In this paper, a polynomial displacement function is developed to evaluate the stability of rectangular thick plate that is freely supported at the third edge and other three edges simply supported (SSFS). Employing three-dimensional (3-D) constitutive relations which consist of entire stress components, the functional for total potential energy was obtained. The governing equations plate was obtained through the variation of the 3-D theory of elasticity to get the slope and deflection relations. The solution of equilibrium equations gives an exact polynomial deflection and rotation function which was gotten after replacement of the variables of total potential energy while the solution of the governing equation gave the expression for the deflection coefficient of the plate. The direct variation method through deflection coefficient was applied to get the formula for calculation of the critical buckling load. Furthermore, the model followed strictly from the first principle of 3-D theory of elasticity without state of stress assumption through the thickness axis of the plate, so that it is able to eliminate the stress under-estimation problem from the approximation and 2-D refined plate theory approach, when the thickness becomes thicker. The result of the present study using the established 3-D model yields an exact solution which shows that it can be used with confidence in the stability analysis of any type of plate boundary condition.

1. Introduction

Plates are three-dimensional structural elements whose parallel plane surface dimensions are large compared with the thickness [1]. In recent times, thick plates have many applications in engineering structures such as offshore platform structures, ship hulls and decks, aircraft wings, building floor, roof, slabs, and spacecraft panels. Hence the research interest in thick plates has greatly increased.

To describe the plate problem in a state of three-dimensional stress, three dimensional theory of elasticity is mostly required [2]. However, plates behavior largely depends on their span-to-depth ratio. Hence, plates are classified as thin, thick or moderately thick plates [3].

According to [4], rectangular plates with 50 ≤ a/t ≤ 100 are classified as thin plate, 20 ≤ a/t ≤ 50 as moderately thick and a/t ≤ 20 as thick plate. 

Thick plate analysis involves research areas such as plate vibration, bending and buckling [5].  Under the influence of in-plane compressive loads, the plate material gradually becomes unstable at the critical value of the loads. This phenomenon is called buckling [6, 7]. Based on the stress – strain relationship, plate buckling problem is classified as elastic and inelastic (plastic) buckling. When the critical buckling load is smaller than the elastic limit of the plate material, it is considered as the elastic buckling problem otherwise the problem is called inelastic buckling [8]. It is therefore necessary to determine the critical buckling loads of a plate to ensure a safe design.  Although the research on plate buckling is still progressive, more attention is drawn to developing and implementing varying methods for solving them depending on the properties of the plate. Generally, the methods employed in solving the buckling problems of plates can be grouped into three namely: classical methods, numerical methods, and the energy methods [9].

The classical methods also called the equilibrium (Euler) methods are analytical methods that seek to obtain closed form solutions for solving the governing partial differential equilibrium equations of the plate buckling problem within the plate domain, subject to the boundary conditions of loading and the restraints of the plate edges [10]. They include the Fourier series method, Navier’s double trigonometric series method, the separation of variables method, and the methods of integral transformation. When applied to plates with fixed edges, free edges and mixed support conditions, mathematical and analytical difficulties are encountered. To obtain approximate solutions to the plate problem, numerical methods are used. These methods include the weighted residual methods, finite difference methods, finite element methods, and finite strip methods [11]. To overcome the rigorous routine inherent in classical and numerical methods, variational method can be applied. The energy methods such as Ritz variational method, Kantorovich variational method, Rayleigh-Ritz method, and Galerkin method; with respect to the displacement function minimizes the total potential energy functional to derive the characteristic buckling equation from which the buckling loads are obtained.

Series of theories has been developed and applied to analyze the buckling behavior of plates. One of these theories is the classical plate theory (CPT) [12], which is mostly employed in the analysis of thin plates, underestimates deflections, and over-estimates buckling loads and natural frequencies in thick plates. Reissner and Mindlin proposed the shear deformation plate theories to overcome the limitations of CPT [12, 13]. These theories are also called the Refined Plate Theories (RPT) which consists of first-order shear deformation theory (FSDT) [14] and higher-order shear deformation theories (HSDT) [15, 16, 17].

FSDT cannot produce accurate results because of the inclusion of a shear correction factor which alters some geometric parameters in the analysis. Reddy’s and Ritz’s theory in HSDT considers the satisfaction of the transverse shear-free surface conditions assuming a parabolic distribution of transverse shear strains throughout the thickness [18, 19, 20]. In this theory, there is no need for shear correction factor. Although these refined plate theories addressed the gap in CPT and are suitable for thick plate analysis, they are inadequate for a three-dimensional plate analysis. A 3-D theory is required for precise analysis of a three-dimensional plate; hence this study is essential.

2. Literature review

The authors in [21] derived the governing plasticity equations using Stowell’s and Bleich’s principles, also formulated the shape function by applying Taylor’s series truncated at the fifth term. The authors in [22] studied rectangular that is clamped at all edges under biaxial compression using Galerkin’s method. Accurate buckling load coefficients were obtained for the same boundary condition using polynomial shape function that was based on Tailor-Mclaurin series. The outcome of their study revealed that the buckling coefficients reduce consistently when the increment in aspect ratios is recorded from 1 to 2, thus, cannot be accurate in predicting the buckling load of thick plate rather thin plate only. They did not consider thick plate assumptions rather limited their study to CPT. More so, both studies failed to cover the plate that is freely supported at the third edge and other three edges simply supported (SSFS) condition and the authors did not consider the use of polynomial functions.

Authors in [23], employed refined trigonometric shear deformation plate theory to analyze the buckling behavior of a simply supported plate under both biaxial and uniaxial compression using the virtual work principle. The result obtained from the study showed excellent agreement when compared with other refined theories.   The exponential shear deformation theory presented by [24] accurately predicted the critical buckling loads of the isotropic thick plates. The use of shear correction factors was unnecessary as the theory took account of transverse shear effects. The authors in [23, 24] did not consider the plate as a typical 3-D plate and could not employ the exact polynomial shear deformation functions in their analysis thereby making their work inexact. The polynomial shape functions were used by the authors in [25, 26] analyzed the buckling behavior of the same thick rectangular plate that is simply supported under uniaxial compressive loading. To derive the governing equations of the plate, the authors applied polynomial shape theory. The equation for formulating the non-dimensional critical buckling load parameters of the plates was obtained by solving the direct governing equation with satisfied plate boundary conditions. The authors in [25] and [26] considered a 3-D theory in their study and applied energy methods in the formulation of governing equation of the plate, but the authors in [25] used an assumed shape function which is not a close-form solution. Both authors failed to take into account the plate with the SSFS edge condition.

To analyze the buckling behavior of clamping plate, the authors in [27] adopted work principle approach. The buckling coefficients of the plate were obtained and a numerical model was developed using the polynomial displacement function. The authors did not take a thick plate into consideration as their assumption is limited to the classical plate theory which is not reliable for thick plate analysis. Their study did not apply trigonometric functions and SSFS plate was not considered. In [28] and [29], the authors applied both trigonometric and polynomial displacement function to determine the critical buckling load of clamped thick rectangular plate using the analytical three-dimensional plate theory that is formulated and derived from the variational energy method, but could not apply it to a rectangular plate structure that is freely supported at the third edge and other three edges simply supported (SSFS).

In the study carried out by [30], the authors applied third order energy functional to analyze the stability of CCSS and CCCS plates within the plate domain and using the combination of the product of the stress and strain at every point in the plate. The authors formulated the third order strain energy equation by incorporating the direct variation method into the third order total potential energy functional which was obtained through the addition of strain energy to the external load. The study did not consider the current shape function and boundary condition or study the plate as a typical 3-D structure which should involve all the six stress element for the thick plate analysis. The authors in [29] applied the variational energy approach to obtain the critical buckling load of a 3-D CSSS thick rectangular plate using a new displacement theory. From the compatibility equation obtained from first principle, the displacement functions were derived and applied in analyzing the plates and this yielded exact solutions. In contrast to refined plate theories, their theory analyzed all the stress elements of the plate, but SSFS thick plate was not taken into account.

The authors in [31] actually studied the static analysis of a three edge simply supported, one support free (SSFS) rectangular thick plate and author in [32] studies thick plate with one edge clamped and other three edges simply supported (CSSS) using RPT. Both authors [31, 32] obtained expressions for the analysis of critical imposed load of the plate at specified limit state or elastic yield stress. They neither determine the critical buckling load that may occur due to compressive load on the plate nor applied an exact 3-D plate theory for reliable results.

The physical properties of SSFS plate material is that, the three edges are supported by a beam and the other remaining edge are free of support, depicting the relevance of the present study. This is because the boundary condition depends on the type of beam/column support in the plate, thus when SSFS initial condition occurs in the a plate material, analyzing it as any other type of plate as mentioned in the literature will not account for stresses induced. This is because, stresses are induced due to the applied load (in-plane load) in this case, and hence, non-negligible error results. Also, the thick plate assumption made in this work made it clear that the deformation line after bending is no longer normal to the mid-plane of the plate thereby considering the effect of shear deformation which may arise if the thickness of the plate are enhanced.

It can be noted in the literature that other shape functions like an exponential, trigonometric and hyperbolic were used, which are not flexible enough to handle all types of plate boundary conditions such as SSFS. This work filled the gap as they applied the variation energy method with a polynomial displacement function to a three-dimensional stability rectangular plate under uniaxial compressive load. Furthermore, compared with previous studies, the distinguishing feature of this current study with other works is that previous studies used an assumed the deflection function while the present study is tends to obtain an exact polynomial deflection function from the equilibrium equation developed.  Apart from the work in [26, 28, 29], no work can be seen that adopted the 3-D plate theory to evaluate the stability of rectangular thick plate. The work in [26, 28, 29] did not study the plate that is freely supported at the third edge and other three edges simply supported (SSFS); so this research work is needed.

This study is focusing on the stability analysis of SSFS rectangular plates section subjected to a uniaxial compressive load using a three-dimensional plate theory with polynomial displacement function. In this work, the aspect ratio effect of the critical buckling load of the plate was evaluated to show its capacity of the derived model to analyze different categories of plate, by presenting a novel formula for determining the critical buckling load of a thick rectangular plate.

3. Methodology

In this work, and displacement in x, y and z axis; u, v and w respectively are applied and presented in Equation (1), (2) and (3) (see [1]):

where; F is deformation profile, 𝜃_x slope in x-axis and 𝜃_y is slope in y-axis of the plate.

It can be seen in figure 1, that the six strains and stress elements required for the analysis were determined in line with the work of authors in [2].

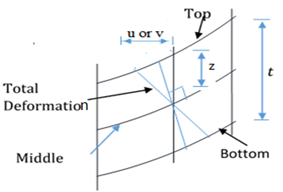
3.1. Formulation of Total Potential Energy

The energy  equation were obtained in line with the authors in [7] and presented as:

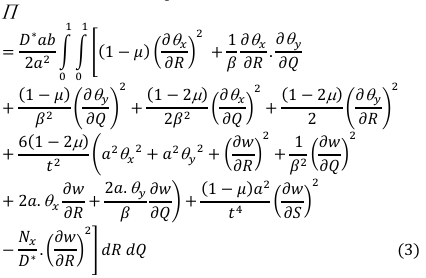
Where; N_x is the uniform applied uniaxial compression load of the plate.

3.2. Compatibility Equations

By differentiation of total potential energy with respect to 𝜃_x and 𝜃_y and establish the relation between the rotation and deflection [8] gives:

where c is a quantity whose expression or value shall be obtained later.

Hence, for zero integrands, the true solution was gotten by simplifying and factorizing the outcome of the compatibility equation to give the algebraic solution in Equation (8) which is the relation of known and unknown variable to get the constant quantity c.

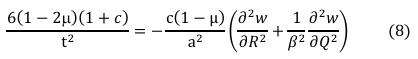
3.3. Governing Equations

The governing differential equation was obtained after the total potential energy was minimized with respect to deflection (w) and its solution yields the exact polynomial deflection function:

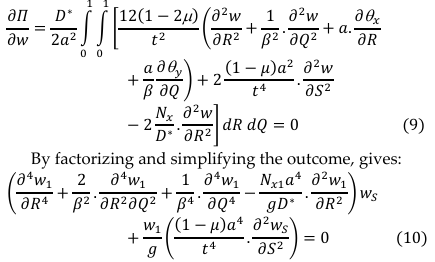
One of the possibilities of Equation (10) to be true is for the terms in each of the two brackets sum to zero. That is:

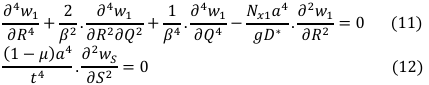
The solution of Equation (11) to get an exact deflection and slope of the plate.

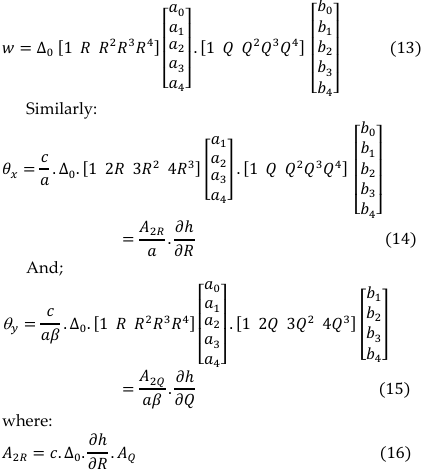
The constants; 𝑐, ∆₀, 𝐴_𝑅 and 𝐴_Q thus, putting Equations (13), (14) and (15) into (3), simplifying gives (see [8]):

Minimizing Equation (18) with respect to A_2R gives:

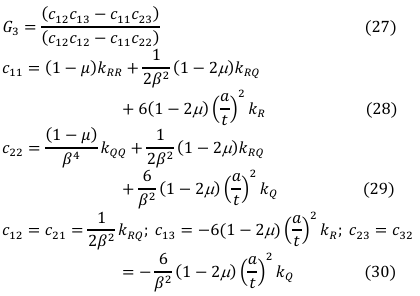
Minimizing Equation (18) with respect to A₁ and simplifying the outcome gives:

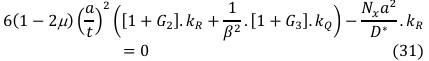
Rearranging Equation (31) and simplify the outcome to gives:

3.4. Numerical Analysis

A numerical analysis is performed on the rectangular thick plate that is freely supported at the third edge and other three edges simply supported (SSFS) under compressive load as presented in the Figure 2.

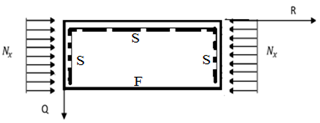
The boundary conditions of the plate in figure 3 are as follows:

Substituting Equations (33-37) into established equation and solving gives the following constants:

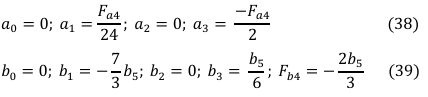
Substituting the constants of Equation (38) and (39) into established equations gives;

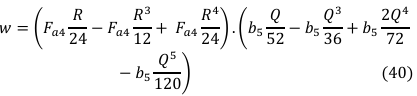
Simplifying Equation (40) which satisfying the boundary conditions of Equation (33-37) gave;

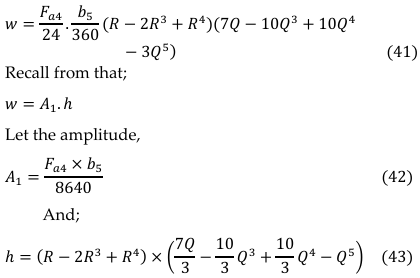
Thus, the polynomial deflection functions after satisfying the boundary conditions is: 

Using the polynomial displacement function, the solution of stiffness coefficients for deflection of rectangular thick plate analysis subjected to the SSFS boundary condition was obtained and presented in Table 1.

Let; the polynomial stiffness coefficient values of SSFS plate 𝑘_𝑅𝑅 = 4.0258; 𝑘_𝑅𝑄 = 1.0331; 𝑘_𝑄𝑄 = 0.1875; 𝑘_𝑅 = 0.4074; 𝑘_𝑄 = 0.10466

Where; the Poisson’s ratio of the plate be 0.3.

4. Results and Discussions

In this section, a numerical solution of the problem of a thick rectangular plate that is freely supported at the third edge and other three edges simply supported (SSFS) presented in Figure 2, is obtained using the Equation presented in the previous section. The non-dimensional value of the critical buckling load for an isotropic SSFS rectangular plate under uniaxial compression is presented in the Figures 1 through 11, different aspect ratio respectively. The numerical and graphical comparison was made to show the disparities between the present study and the literature under review to show the effect of aspect ratio on the buckling load in a 3-D stability analysis of rectangular plate at varying thickness. The span to thickness ratio considered is ranged between 4 through 1500, which is obviously seen to span from the thick plate, moderately thick plate and thin plate (see [4]). On the other hand, the length and breadth ratio (aspect ratio) in consideration in this study includes; 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5 and 5.0. Meanwhile, in this study, more attention is to be given to the effect of aspect ratio on the buckling load for thicker plate. This is because, the effect of shear deformation was considered in the analysis, and that made it possible to predict accurately the buckling load of any type of plate ranging from thin through thick plate.

The present work obtained non-dimensional result of buckling load of the plate by expressing the displacement function of the plate in the form of polynomial to analyze the effect of aspect ratio of the critical buckling load of the plate. Figure 3 in Figure 11 contains the graphical representation of the result of the non-dimensional critical buckling load SSFS rectangular thick plate using the established exact polynomial displacement function. The value of the critical buckling load N_xcr decreases as the aspect ratio of the plate increases, as shown in Figure 3 to Figure 11, the value of critical buckling load decreases. This means that the failure in a plate structure is bound to occur as the in-plane load on the plate increases and gets to the critical buckling.

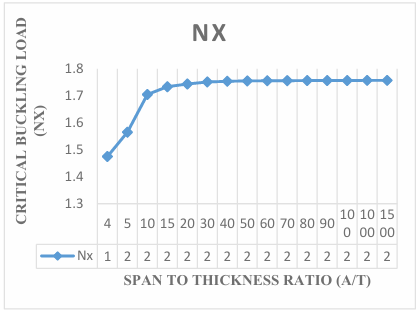
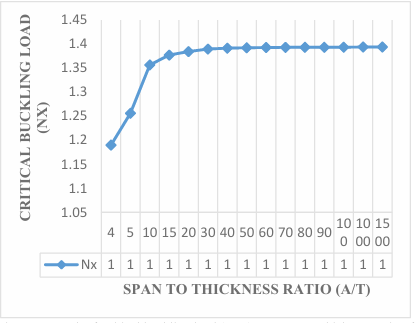
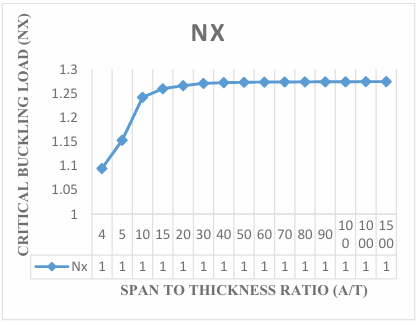
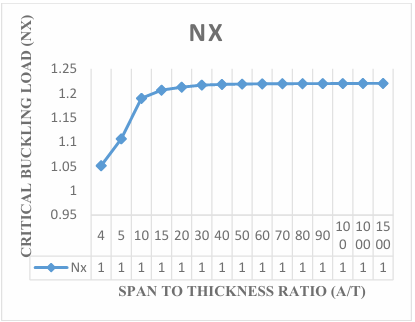
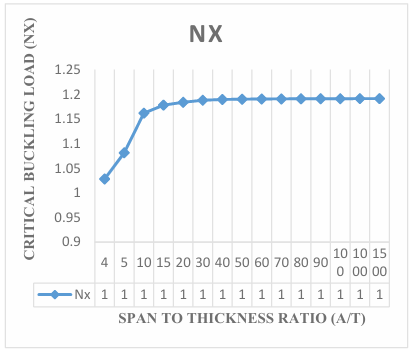
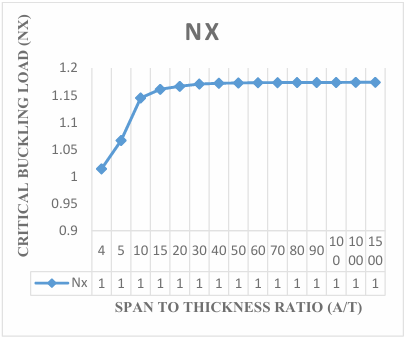
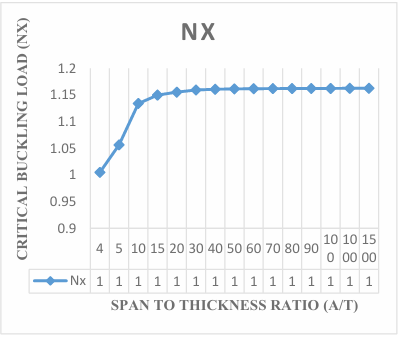
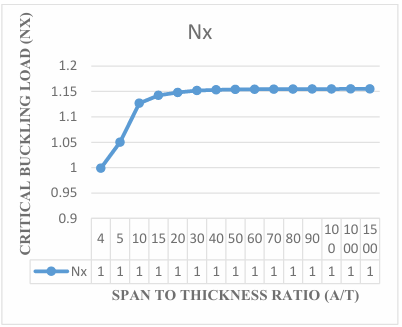
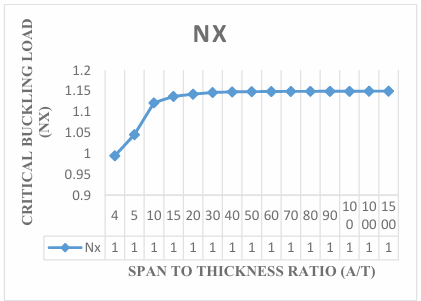
The results obtained in the Figures reveals that the values of critical buckling load increase as the span- thickness ratio increases. This reveals that as the span or the depth of the plate is altered, it affects the performance in terms of the serviceability of the plate. Thus, caution must be taken when selecting the depth and other dimensions along the x and y co-ordinate of the plate to ensure safety and accuracy of the analysis.

The present theory predicts the buckling load of 1.29, 1.50, 1.52, 1.53, 1.54, 1.54, 1.54, 1.54, 1.54, 1.54, 1.54, 1.54, 1.54 and 1.54 for a square plate in the span to thickness ratio of 4, 10, 15, 20, 30, 40, 50, 60, 70, 80, 90, 100, 1000 and 1500. Looking closely at the result of buckling load for the present study at the span to thickness ratio of 30 and beyond, it is seen that the value of critical buckling load of the plate maintained a constant value of 1.54 for square plate, 1.22 for aspect ratio of 1.5, 1.11 for aspect ratio of 2.0, 1.07 for aspect ratio of 2.5, 1.04 for aspect ratio of 3.0, 1.03 for aspect ratio of 3.5, 1.02 for aspect ratio of 4.0, 1.01 for aspect ratio of 4.5, 1.01 for aspect ratio of 5.0. This shows that the result of the critical buckling load of thin and moderately thick plate using the 3-D theory is the same for the stability analysis of rectangular plate under the SSFS boundary condition. The Figures 3 to 12 proofs that the value of critical load for thin plate and thick plate (see [29]) which described the thin and moderately thick plate as the one whose span to thickness ratio is equal or less than 30.

It can be deduced that the present model using a derived shape function is safer and more credible to use as it considered the six stress elements to yield the exact solution for the analysis of thick plate that is freely supported at the third edge and other three edges simply supported (SSFS). Hence, the result of the present analysis, which contains all the stress element and ensured that the variation of the stresses through the thickness of the plate which induced buckling are uniformly distributed, showed that the present method can be used with confidence for stability analysis of plate.

5. Conclusion

The buckling of an isotropic thick plate that is freely supported at the third edge and other three edges simply supported (SSFS), was investigated. The 3-D theory using energy methods with polynomial shape function was employed. The solution obtained showed a good agreement with results from previous works.  It is observed that the classical plate theories give reliable results for thin plates, refined plate theories the 2-D refined plate theory (RPT) is only an approximate relation for buckling analysis of thick plate and when applied to the thick plate will under-predicts buckling loads as they neglect the transverse normal stresses along the thickness axis of the plate while 3-D theory with exact shape functions developed in this study yield exact solution for the buckling analysis of thick plates.

6. Recommendation

The polynomial displacement function developed in this study produces an exact solution as they emanated from a complete three-dimensional theory which is more reliable solution in the stability analysis of plates and, can be recommended for analysis of any type of rectangular plate subjected to such loading and boundary condition.

7. Contribution to Knowledge

The major contribution to knowledge in this study is the novel formula for calculating the critical buckling load of the plate which was derived from the principle of elasticity and satisfied SSFS boundary condition when solved with polynomial shape function.

The exact deflection and slope model which was established from the 3-D stability analysis derived from equilibrium equation using static elastic theory to get exact polynomial displacement functions of the plate.

1. F. C. Onyeka, B. O. Mama, T. E. Okeke, “Elastic Bending Analysis Exact Solution of Plate using Alternative I Refined Plate Theory,” Nigerian Journal of Technology (NIJOTECH), vol. 40, no. 6, pp. 1018 –1029, 2021. doi: http://dx.doi.org/10.4314/njt.v40i6.4
2. F. C. Onyeka, B. O. Mama, “Analytical Study of Bending Characteristics of an Elastic Rectangular Plate using Direct Variational Energy Approach with Trigonometric Function,” Emerging Science Journal, vol. 5, no. 6, pp. 916–926, 2021. doi: 10.28991/esj-2021-01320
3. K. Chandrashekhara, Theory of Plates, University Press (India) Limited, 2000.
4. F. C. Onyeka, F. O. Okafor, H. N. Onah, “Application of Exact Solution Approach in the Analysis of Thick Rectangular Plate,” International Journal of Applied Engineering Research, vol. 14, no. 8, pp. 2043-2057, 2019.
5. F. C. Onyeka, E. T. Okeke, “Analytical Solution of Thick Rectangular Plate with Clamped and Free Support Boundary Condition using Polynomial Shear Deformation Theory,” Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 1427-1439, 2021, doi:10.25046/aj0601162..
6. A. Hassan, N. Kurgan, “Modeling and Buckling Analysis of Rectangular Plates in ANSYS,” International Journal of Engineering & Applied Sciences (IJEAS), vol. 11, no. 1, pp. 310-329, 2019. doi: http://dx.doi.org/10.24107/ijeas.531011.
7. F. C. Onyeka. B. O. Mama, C. D. Nwa-David, “Analytical Modelling of a Three-Dimensional (3D) Rectangular Plate Using the Exact Solution Approach,” IOSR Journal of Mechanical and Civil Engineering (IOSR-JMCE), vol. 19, no. 1 Ser. I, pp. 76-88, 2022. doi: 10.9790/1684-1901017688.
8. F. C. Onyeka, F. O. Okafor, H. N. Onah, “Buckling Solution of a Three-Dimensional Clamped Rectangular Thick Plate Using Direct Variational Method,” IOSR Journal of Mechanical and Civil Engineering (IOSR-JMCE), vol. 18, no. 3, pp. 10-22, 2021, doi: 10.9790/1684-803031022.
9. S. P. Timoshenko, J. M. Gere, W. Prager, Theory of Elastic Stability, Second Edition. In Journal of Applied Mechanics (2nd ed.), vol. 29, no. 1, McGraw-Hill Books Company, 1962. doi:10.1115/1.3636481.
10. F. C. Onyeka, D. Osegbowa, E. E. Arinze, “Application of a New Refined Shear Deformation Theory for the Analysis of Thick Rectangular Plates,” Nigerian Research Journal of Engineering and Environmental Sciences, vol. 5, no. 2, 901-917, 2020.
11. C. C. Ike, “Kantorovich-Euler Lagrange-Galerkin’s Method for Bending Analysis of Thin Plates,” Nigerian Journal of Technology (NIJOTECH), vol. 36, no. 2, pp. 351-360, 2017.
12. J. N. Reddy, Classical Theory of Plates, In Theory and Analysis of Elastic Plates and Shells, CRC Press, 2006. doi: 10.1201/9780849384165-7.
13. F. C. Onyeka, O. M. Ibearugbulem, “Load Analysis and Bending Solutions of Rectangular Thick Plate,” International Journal of Emerging Technologies, vol. 11, no. 3, pp. 1030-1110, 2020.
14. R. D. Mindlin, “Influence of Rotatory Inertia and Shear on Flexural Motions of Isotropic, Elastic Plates,” J. Appl. Mech. Trans. ASME, vol. 18, no. 1, pp. 31-38, 1951.
15. F. C. Onyeka, E. T. Okeke, J. Wasiu, “Strain–Displacement Expressions And Their Effect On The Deflection And Strength Of Plate,” Advances in Science, Technology and Engineering Systems, vol. 5, no. 5, pp. 401-413, 2020, doi:10.25046/AJ050551.
16. A. S. Sayyad, Y. M.  Ghugal, “Bending and Free Vibration Analysis Of Thick Isotropic Plates By Using Exponential Shear Deformation Theory,” Journal of Applied and Computational Mechanics, vol. 6, pp. 65-82, 2012.
17. F. C. Onyeka, B. O. Mama, C. D. Nwa-David. “Application of Variation Method in Three Dimensional Stability Analysis of Rectangular Plate Using Various Exact Shape Functions.” Nigerian Journal of Technology, vol. 41, no. 1, pp. 8-20, 2022. doi: http://dx.doi.org/10.4314/njt.v41i1.2
18. J. N. Reddy, N. Phan, “Stability and Vibration of Isotropic, Orthotropic and Laminated Plates According to a Higher-Order Shear Deformation Theory,” Journal of sound and vibration, vol. 98, no. 2, pp. 157-170, 1985.
19. F. C. Onyeka, O. T. Edozie, “Application of Higher Order Shear Deformation Theory in the Analysis of thick Rectangular Plate,” International Journal on Emerging Technologies, vol. 11, no. 5, pp. 62-67, 2020.
20. F. C. Onyeka, T. E. Okeke, “New Refined Shear Deformation Theory Effect On Non-Linear Analysis of A Thick Plate Using Energy Method.” Arid Zone Journal of Engineering, Technology and Environment, vol. 17, no. 2, 121-140, 2021.
21. D. O. Onwuka, U. G. Eziefula, O. M. Ibearugbulem, “Inelastic Buckling of Rectangular Panel with a Simply Supported Edge and Three Clamped Edges,” International Journal of Applied Science and Engineering, vol. 14, no. 1, pp. 39-48, 2016.
22. S. E Iwuoha, “Biaxial Buckling Coefficients of Thin Rectangular Isotropic Plates, Having One Edge Simply Supported and The Other Edges Clamped,” International Journal of Scientific & Engineering Research, vol. 9, no. 7, pp. 1918-1925, 2018.
23. S. M. Gunjal, R. B. Hajare, A. S. Sayyad, M. D. Ghodle, “Buckling Analysis of Thick Plates Using Refined Trigonometric Shear Deformation Theory,” Journal of Materials and Engineering Structures, vol. 2, pp. 159-167, 2015.
24. A. S. Sayyad, Y. M. Ghugal, “Buckling Analysis of Thick Isotropic Plates by Using Exponential Shear Deformation Theory,” Applied and Computational Mechanics, vol. 6, pp. 185-196, 2012.
25. J. C. Ezeh, I. C. Onyechere, O. M. Ibearugbulem, U. C. Anya, L. Anyaogu, “Buckling Analysis of Thick Rectangular Flat SSSS Plates using Polynomial Displacement Functions,” International Journal of Scientific & Engineering Research, vol. 9, no. 9, pp. 387-392, 2018.
26. F. C. Onyeka, B.O. Mama, T. E. Okeke, “Exact Three-Dimensional Stability Analysis of Plate Using A Direct Variational Energy Method,” Civil Engineering Journal, vol. 8, no. 1, pp. 60–80, 2022. DOI: 10.28991/CEJ-2022-08-01-05.
27. V. T. Ibeabuchi, O. M. Ibearugbulem, C. Ezeah, O. O. Ugwu, “Elastic Buckling Analysis of Uniaxially Compressed CCCC Stiffened Isotropic Plates,” Int. J. of Applied Mechanics and Engineering, vol. 25, no. 4, pp. 84-95, 2020. doi: 10.2478/ijame-2020-0051.
28. F. C. Onyeka, F. O. Okafor, H. N. Onah, “Buckling Solution of a Three-Dimensional Clamped Rectangular Thick Plate Using Direct Variational Method,” IOSR Journal of Mechanical and Civil Engineering (IOSR-JMCE), vol. 18, no. 3 Ser. III, pp. 10-22, 2021.  doi: 10.9790/1684-1803031022.
29. F. C. Onyeka, F. O. Okafor, H. N. Onah, “Application of a New Trigonometric Theory in the Buckling Analysis of Three-Dimensional Thick Plate,” International Journal of Emerging Technologies, vol. 12, no. 1, pp. 228-240, 2021.
30. S. Uzoukwu, O. M. Ibearugbulem, C. E. Okere, J. I. Arimanwa, “Stability Analysis of Rectangular CCSS and CCCS Isotropic Plates using 3rd Order Energy Functional,” Global Scientific Journals, vol. 9, no. 1, pp. 637-649, 2021.
31. F. C. Onyeka, C. D. Nwa-David, E. E. Arinze, “Structural Imposed Load Analysis of Isotropic Rectangular Plate Carrying a Uniformly Distributed Load Using Refined Shear Plate Theory,” FUOYE Journal of Engineering and Technology (FUOYEJET), vol. 6, no. 4, pp. 414-419, 2021. doi: 10.46792/fuoyejet.v6i4.719.
32. F. C. Onyeka, “Critical Lateral Load Analysis of Rectangular Plate Considering Shear Deformation Effect,” Global Journal of Civil Engineering, vol. 1, pp. 16-27, 2020. doi: 10.37516/global.j.civ.eng.2020.0121.

Citations by Dimensions

Citations by PlumX

Crossref Citations

This paper is currently not cited.

No. of Downloads per Month

No. of Downloads per Country