The main goal of the work was the development of software and codes for the design of new generation nuclear reactors. The problem is solved by the example of fast reactors with a liquid metal coolant. The problem is solved within the framework of system analysis methods and operations drawing methods. Three groups of methods for solving the problem can be distinguished: optimization methods, methods for calculating stationary states, methods for simulating emergency modes. When designing safe fast reactors, ATWS emergency modes and their combinations are primarily considered. All ATWS modes are grouped into five groups: TOP WS (Transient Overpower without Scram); LOF WS (Loss of Flow without Scram); OVC WS (Overcooling Accident without Scram); LOHS WS (Loss of Heat Sink without Scram) and LOCA WS (Loss of Coolant Accident without Scram). A number of auxiliary discrete multicriteria problems have been solved. To solve them, the method of displaced ideal, lexicographic methods, and maximin strategy of cooperative play were used. Decomposition methods are widely used in research. To solve the multicriteria (two-criterion) problem of continuous optimization, a strategy of sequential decision-making in positional games was used. As a result, a number of codes have been developed that collectively implement the decision-making methodology in the design of nuclear reactors. Among the auxiliary problems, the problems of optimizing the composition of the lead coolant, the problem of optimizing the choice of the fuel composition and structural materials are solved. The choice of parameters that have the greatest impact on the safety of a high-power reactor with a lead coolant is carried out. The proposed algorithms, procedures, methods and codes contribute to solving the problem of designing safe reactors of a new generation – energy sources that will provide human energy on the required scale for the long term.

1. Introduction

1.1. Background

Increased energy consumption is helping to increase the world’s population and meet the growing human needs for a better quality of life. Traditional sources of energy are based on the combustion of hydrocarbon fuels. Such fuel is extremely unevenly distributed in the earth’s crust. This is the source of conflicts and wars between states. In addition, it requires the transportation of large volumes of fuel. The use of hydroelectric power plants leads to the alienation of territories and climate change in certain regions of the world. Hydroelectric power plants account for from 5.2% in the Middle East to almost 51% in Central and South America [1]. More than 60% of all electricity in the world is generated at thermal power plants, about 20% at hydroelectric power plants, about 17% at nuclear power plants and about 1% at geothermal, tidal, solar and wind power plants [2].

The development of safe nuclear energy contributes to the solution of a number of key problems. Among these tasks, the following are the most important:

• Providing mankind with energy for the long term;
• Economic growth;
• Ensuring energy security of the states of the world;
• Elimination of greenhouse gas emissions and environmental pollution (introduction into the biosphere or appearance in it of new, usually uncharacteristic physical, chemical or biological pollutants, exceeding their natural level);
• Exclusion of alienation of territories during the construction of hydroelectric power plants;
• It is possible to achieve high energy release, “compact” fuel processing (at one site) and minimize the amount of fuel used.

These tasks can be solved by ensuring the internal security of nuclear fuel cycle enterprises and, first of all, nuclear reactors of a new generation. The elimination of accidents at nuclear power plants is possible when using, for example, liquid metal fast reactors (LMFRs) with innovative cermets fuel based on mononitride micro grains UN-PuN (or UN) and a coolant based on lead extracted from thorium ores (with a ²⁰⁸Pb isotope content of at least 75 … 80 %) [3].

In Russia, a project has been developed for the BREST-OD-300 reactor with mononitride fuel and lead coolant [4], the construction of which began in 2021.

1.2. Relevance of Research

The relevance of research is determined by the need for safety analysis (first of all, to exclude severe accidents) at the stage of conceptual development of the reactor. This is possible due to the appropriate choice of the composition and geometry of the core. Deterministic exclusion on this basis of severe accidents will minimize the risk of unacceptable releases of radioactive materials outside the station to practically zero.

In Russia, by the middle of the XXI century, a transition to large-scale nuclear power is predicted [4]. This will require a shift in the priorities for the development of nuclear power in the direction of increasing the self-protection of nuclear reactors. This is possible on the basis of the development of new computational and optimization research methods. Identify the techniques required primarily for innovative reactor designs and concepts, including LMFRs. Fast reactors are considered as promising structures for large-scale nuclear power. Research requires the solution of core optimization problems with constraints, including for functionals that characterize the entire set of emergency modes that are not deterministically excluded (safety functionals). First of all, emergency modes of the ATWS type (anticipated transient without scram) are considered [3].

The author considered five groups of emergency modes from among ATWS (and their combinations) [5, 6]:

• Transient Overpower without Scram (TOP WS);
• Loss of Flow without Scram (LOF WS);
• Overcooling Accident without Scram (OVC WS);
• Loss of Heat Sink without Scram (LOHS WS);
• Loss of Coolant Accident without Scram (LOCA WS).

Preliminary results of research in this area are presented in publications [3, 6].

2. Methods

2.1. Research Methods and Tasks

The reactor core is considered as a system of many elements in communication with each other [6]. The study of such systems is carried out within the framework of systems analysis and is solved on the basis of methods for researching operations associated with the construction, development and application of mathematical decision-making models. The decision-making model in the problem of creating a safe reactor has a large dimension, contains heterogeneous (numerical, logical, lexical) information, fuzziness, uncertainty, incompleteness, and others. In this regard, the rationalization (increase in efficiency) of the decision-making procedure has been carried out. The requirement for deterministic elimination of severe accidents is formalized in the form of restrictions for a number of safety functionalities corresponding to the preservation of the operability of safety barriers [3, 6]. In game theory, the problem of optimal design of a reactor, in which severe accidents are deterministically excluded, can be formulated as a game with a thinking adversary, which, in turn, with appropriate formalization of some intuitive concepts, can be reduced to solving a number of problems with varying degrees of formalization.

In practice, the design tasks for rectors can be classified as partly integer optimization problems. The following tasks are considered (in decreasing order of formalization), which form the basis of a unified methodology [3, 6].

Problems of mathematical programming in a deterministic setting allow you to get a single optimal solution. It is required to determine the control vector

u = {uk} = ? (k = 1, 2,…, K).

The domain of definition of the control vector is

uk^min ≤ uk ≤ uk^max.

The optimality criterion is

F0 (u) → opt (min or max),

There are task restrictions

Fi (u) ≤ Fi *, i = 1, 2,…, I;

here F_i^* are the maximum admissible values of the corresponding functionals. The functionals F₀ and F_i  also depend on state variables. These variables satisfy the known equations. As F₀ and F_i functionals are considered that characterize the basic requirements for energy sources of the future:

○ Safety,

○ Self-sufficiency in fuel,

○ Cost-effectiveness.

The control vector u includes the characteristics of the core.

For the first time, the problem of complex optimization of the core of a fast reactor, taking into account the constraints on neutron, thermo hydraulic and strength characteristics, ensuring reliable operation of the reactor at a given power, was solved by V.V. Khromov, A.M. Kuzmin and V.V. Orlov [7]. They proposed an iterative optimization method – the method of sequential linearization [7].

The author of this work has expanded the range of problems to be solved with the help of the developed auxiliary codes that allow solving the following problems:

it is necessary to take into account in the optimization studies the safety functionals that characterize the entire set of emergency situations;

○ it is necessary to take into account in the optimization studies the safety functionals that characterize the entire set of emergency situations;

○ solving problems without an optimality criterion for finding the area of safe layouts;

○ taking into account the uncertainty of scenarios for the development of emergency situations;

○ post-optimization analysis;

○ auxiliary applied multicriteria problems (see below).

The properties of the core materials were included in the control parameters. This made it possible to develop reactors with specified safety properties.

• Mathematical programming problems with undefined data v provide many solutions. The task is formulated as follows:

u = {uk} = ? (k = 1, 2,…, K);

uk^min ≤ uk ≤ uk^max;

F₀ (u, v) → opt;

F_i (u, v) ≤ Fi * (v); i = 1, 2,…, I.

The functionals F₀ and F_i also depend on state variables. These variables satisfy the known equations.

By the end of the 1970s, L.S. Popyrin and others (Siberian Branch of the Academy of Sciences of the USSR) formulated methodological provisions for the implementation of optimization calculations in the power industry with the ambiguity of the initial data. In the 1980s, the staff of MEPhI, IPPE, and the Kurchatov Institute, using the simplest codes, obtained estimates of the effect of uncertainties in the initial data on the optimal layout of a fast reactor (without taking into account safety).

• The following applied multicriteria problems were solved [6].

○ In order to reduce the dimension of the optimal design problem and justify the safety of the reactor, based on the analysis of conflicts, the most significant safety functions are selected. The author proposes a hierarchical model for the study of conflicts, ways of overcoming them.

○ On the basis of the maximin principle, the tasks of ranking emergency situations according to the degree of hazard in reactors of different types were solved. The degree of hazard corresponds to the degree of significance from the point of view of the priority consideration of one or another emergency mode in the problems of optimal design.

○ the problem of ranking the coolants of fast reactors according to the degree of preference was solved using lexicographic methods.

○ The two-criterion problem of continuous optimization of a fast reactor for maximum power and minimum void reactivity effect with restrictions for various functionals, including safety functionals, was solved using the Dragon-M code, which was repeatedly modernized by the author, based on a multi-step decision-making procedure.

○ Discrete multicriteria problems of choosing the most preferable lead deposits with a high content of the ²⁰⁸Pb isotope, choosing preferred (including conditionally equally safe) core layouts, ranking reactor parameters according to the degree of impact on reactor safety, are solved by the shifted ideal method. The algorithm of the method is presented in [8].

• To reduce the dimension of the optimization problem, including by identifying emergency situations that neutralize and aggravate each other (when they are superimposed) and exclude interrelated criteria, elements of the non-formalized theory of conflict were used.

To solve multicriteria problems, the well-known methods [8-10] and these methods, modified by the author, are used.

It is necessary to note the personal contribution of the author and the novelty of the article.

The Dragon code for complex calculation and optimization of fast reactors was developed at MEPhI (Russia) in the mid 1990s. Its authors are N.I. Geraskin, A.M. Kuzmin, D.V. Morin, A.E. Novikov and V.S. Okunev. The code did not take into account the functionals characterizing the safety of the reactor (safety functionals). For this reason, an upgrade of the Dragon code was required. Modernization of the Dragon code (Dragon-M) was carried out by the author.

The author formulated and included in the optimization code the functionals characterizing the emergency modes of the reactor. The author has developed the FRISS code for simulating emergency modes (including ATWS and their combinations). One version of the FRISS code can work as part of the Dragon optimization code. Combining all emergency modes into a small number of groups is a well-known approach proposed by the authors from Argonne National Laboratory (US DOE) in experiments on EBR-II [5]. Methods for combining emergency modes into groups are known and generally accepted [5].

Research experience has shown that the problem with restrictions on safety functionals does not have a solution for all existing nuclear reactors and most projects of new generation reactors. It has solutions for lead-cooled fast reactors.

The last update to the Dragon-M code was to expand the list of control parameters. Their composition included the properties of the core materials (density, thermal conductivity, heat capacity, neutron interaction cross sections). Modernization carried out by the author. When obtaining the optimal option, it was necessary to select materials with the necessary (optimal or acceptable) properties. This procedure was also carried out by the author.

The author proposes an algorithm (procedure) for making decisions. Similar procedures are commonly used in such studies. It can be considered generally accepted.

In order to refine the optimization results, the author has developed hierarchical models with adjustable accuracy based on the precision MCU code. The need to refine the results obtained using approximate models is known and generally accepted. In this work, it is necessary to clarify the values of the void effect of reactivity. In an inhomogeneous core, the diffusion approximation (adopted in the Dragon-M code) can give rough results. In order to refine the optimization results, the author has developed hierarchical models with adjustable accuracy based on the precision MCU code. The need to refine the results obtained using approximate models is known and generally accepted. In this work, it is necessary to clarify the values of the void effect of reactivity. In an inhomogeneous core, the diffusion approximation (adopted in the Dragon-M code) can give rough results.

2.2. Research Directions

To solve the problems of searching for the physical characteristics of the core of a fast reactor, research has been carried out in the following areas.

• Computational and optimization studies of the core of fast reactors of a new generation, including the development of effective models that take into account the constraints for safety functional, characterizing the totality of the most dangerous emergency situations.
• Post-optimization analysis for deterministic justification of the safety of fast reactors, including the development of models with adjustable accuracy based on precision neutron-physical calculations programs, and their use for exploratory computational experiments.
• Post-optimization analysis, which implies the development of effective models for comparing optimal reactor layouts according to different criteria and choosing the most preferable of them (conditionally equally safe).

The studies involve taking into account the uncertainty of scenarios for the development of emergency situations. In order to rationalize the decision-making procedure in the tasks of the initial design stage, substantiation and analysis of reactor safety, the methods, models, approaches and procedures proposed and implemented by the author are combined into a single methodology based on a systematic approach [6].

2.3. Decision Making Procedure. The Knowledge Base is the Basis for Making Decisions

Decision-making in the design problems of a new generation reactor presupposes the complex use of natural (human) and artificial (computer) intelligence. Routine operations, mainly related to the analysis and processing of numerical data, are performed by a computer. The volume of lexical information is relatively small and the human intellect can easily handle it. If necessary (although such a need is questionable) in the decision-making process, you can find a “niche” for the use of technical neural networks. In the general case, the decision-making procedure is possible using natural or technical neural networks. The final decision on the choice of the reactor layout option, which will subsequently be implemented (built), is made by a person.

It is possible to propose a decision-making procedure based on the sequential execution of a number of stages [6]. At the same time, it is formally convenient to distinguish three levels of the hierarchy of decision-makers. At the top level of the hierarchy, a decision is made (approved) by an official (for example, in Russia, this is the head of Rosatom State Corporation), who is in control of the situation as a whole and is able to pose the problem in the most general form (without mathematical formalization) and intuitively (for example, by a strong-willed decision, or on the basis of voting in the case of a collegial decision) to choose the most preferable (he liked) option, which will subsequently be implemented.

In order to minimize errors in decision-making at the upper hierarchical level, one of the main tasks of a decision-maker, the second (intermediate) level of the hierarchy, is to minimize the number of options transferred to the upper level and maximally facilitate the analysis of options through, for example, preliminary ranking of these options for a particular set of quality criteria. This will not only minimize errors, but also reduce the decision-making time at the top level of the hierarchy.

Such a global analysis practically does not require from the decision maker, the top level of specific training in the field of solving specific narrow-profile technical problems and problems of applied mathematics. The decision-maker at the second level of the hierarchy can be a team of experts – specialists in the field of nuclear technologies, systems analysis and control theory. The quality of the decisions made (there is a term – the reliability of the decisions made) at the second and third levels of the hierarchy directly depends on the professional qualifications of the decision maker.

The third (lower) level of the hierarchy of the decision-maker consists of teams of specialists in various fields of knowledge who, through interaction, are able to comprehensively solve the entire range of narrow-profile physical and mathematical, technical, technological, design and other problems. Their main task is to formulate, solve and analyze the results of a specific narrow-profile task.

Generally speaking, all decisions can be made by one specialist or a relatively small team of specialists who are proficient in decision-making theory and the appropriate physical and mathematical methods and design skills. This often happens, for example, in the preparation of conceptual projects for new generation reactors. In this case, the decisions made can be conditionally divided into three levels of hierarchy.

A similar procedure is implemented in the problems of optimal design of fast reactors of a new generation based on the computational and optimization program code “Dragon-M”, i.e., in the general case, some computational and optimization code should serve as the base or the core of the decision making procedure.

In the proposed decision-making procedure, four knowledge bases are used sequentially. The knowledge (data) base is understood as an organized body of knowledge (data) intended for their storage, accumulation and processing using a computer.

• An external common (global) knowledge base represents the entire set of research results in the field of traditional, non-traditional and innovative nuclear technologies, all the experience accumulated by the scientific community over more than 60 years of development of these technologies. Such a “base” (in quotation marks, since such a unified and complete base on nuclear technologies does not yet exist) can be an information retrieval thesaurus that includes heterogeneous (lexical, numerical, graphic) information with a specific (given) system of semantic relations.

The base is considered “external”, since its existence is assumed even before the design of a specific reactor and such a base, generally speaking, has nothing to do with the design of the reactor (it exists by itself and is replenished as new technologies develop). Today, for example, specialized encyclopedias, including electronic ones, monographs and other sources, can act as an external base. (As an example of the most common base, one can consider, for example, the information presented on the IAEA (International Atomic Energy Agency) website [11].

Information retrieval thesauri became widespread in the 1970s. The search for the necessary information is carried out automatically according to the special lexical units specified by the user – descriptors. Such thesauri usually contain semantic maps of thematic classes. This is perhaps the only niche for using neural networks in the problem of reactor design. Technical neural systems and the neural network approach in general can greatly facilitate the search for the necessary information by specifying by the user of such a neurosaurus (network) practically any, including fuzzy, semantic relations associated with a given problem.

Information from this external base is used mainly at the stage of the general statement of the problem and determination of the purpose of the decision-making. However, if necessary, an appeal to an external base is possible at any stages of decision-making by a decision-maker, at any level of the hierarchy. (For example, to correct decisions.)

The other three knowledge bases are internal. They are filled in during the design of a specific reactor, that is, they are formed in the process of consistent decision-making. They are necessary for making a decision in a specific case, for solving a specific problem and contain much less information. This volume is also decisive in making a decision about the necessity, possibility (expediency) or unreasonableness (inexpediency) of using the neural network approach. These databases are data files containing heterogeneous information. Separate information from internal databases (files) can go to the global external knowledge base on nuclear technologies.

Depending on the convenience of use, the three internal databases can be combined into a single internal information base, which is used to solve a specific problem – the problem of optimal reactor design.

2.4. Algorithm (Procedure) for Making Decisions

The decision-making algorithm in the problems of optimal design of a safe reactor includes the following stages.

1. Statement and analysis of the problem situation, and the definition of the general goal of research and decision-making. The stage is in the competence of the person making the decision of the upper hierarchical level, and contains mainly lexical information about some of the most significant properties of the designed object (reactor and NPP) and the main requirements for it. The initial information comes from an external knowledge base. The resources of the IAEA can be used as such a base [12, 13]. These resources are well organized and contain scientific and technical publications and other documents. A user-friendly interface and a logical clear hierarchical structure allow you to quickly search for the necessary information. The processed information goes to the first internal database.

2. Formation of a system of quality criteria and mathematical formalization of the design problem statement. At this stage, information from the external knowledge base on nuclear technologies is used and the first internal database is updated with information. The stage is in the competence of the decision maker, the second level of the hierarchy.

3. Reduction of the original multicriteria reactor design problem to various mathematical programming problems. This stage is performed by the third level decision-maker. The ranking of possible criteria according to the degree of prediction is carried out on the basis of general considerations – an external knowledge base (it is customary to optimize power reactors according to one of the autonomic criteria, for example, the cost of electricity produced) and information obtained from the first internal database. The problem associated with the large dimension of the problem can also be solved on the basis of preliminary ranking of the functionals of the problem according to the degree of significance or the importance of influence on the results of solving a specific problem. A possible way of ranking emergency situations and safety functionals according to the degree of significance was developed by the author on the basis of the maximin strategy of a cooperative game. The probabilities of accidents, safety functionals and others were chosen as criteria for a discrete multicriteria problem. Emergency modes from among ATWS and their combinations were selected as objects of the problem.

4. Solving problems of mathematical programming, including in conditions of uncertainty of the initial information. The stage is implemented by the decision maker of the third level of the hierarchy using the basic computational and optimization software package (in this case: when designing fast reactors, it is proposed to use the “Dragon-M” code [3, 6]. The solution to the problem of mathematical programming is fully formalized. However, the obtained optimum may turn out to be local. A single (global) optimum is needed. For this reason, the problem of mathematical programming is usually solved several times, using different initial values of the control parameters. If the solutions coincide, the found optimum is global, that is, it is defined correctly.

5. Analysis of solutions to problems of mathematical programming. If necessary, the stage includes a parameterization procedure, an analysis of uncertainties, an additional “extended” safety analysis, involving consideration of a wider set of emergency situations that were deliberately excluded from consideration at the previous stage when choosing the most significant emergency modes and functionalities characterizing these modes. The ranking of decisions according to the degree of preference is carried out with the aim of possible exclusion from consideration of uninformative or obviously unpreferable options. All results are consolidated into a single database (second internal database). This stage is performed by the decision maker of the third hierarchical level.

6. Determination of a set of additional criteria (including on the basis of internal knowledge bases) for choosing preferred options, establishing the preference of criteria, formulating a multi-criteria problem. The stage is performed by the decision maker at the second level of the hierarchy.
7. Solving the multicriteria problem posed at the previous stage using different methods. The analysis of the stability of the solution to the chosen methods is carried out. The preferred options are determined. The stage is implemented by the decision-maker of the third hierarchical level.

8. Additional analysis of the results is underway. It is based on high-precision (precision) calculations using the appropriate software sysJtems and correcting the options obtained in the previous stage.
9. An analysis of the preferred options obtained in the previous steps is carried out. The ranking of options according to the degree of preference is given from the point of view of a particular set of criteria. In this case, previously excluded (less significant) information from internal knowledge bases is used. A third internal database is being formed with comments on each option and each chain of options, arranged in the order of certain priorities. The stage is performed by a second-level decision maker.
10. Transfer of the third internal database to the upper level of the hierarchy for the final decision: the choice of the only option that will be implemented.

2.5. Optimization Models

The decision-making procedure is based on the “Dragon-M” calculation and optimization code.

The search for the optimum is carried out using the method of sequential linearization [7]. This method has been successfully used for several decades to solve practical problems of optimizing fast reactors. The method of penalty functions can be considered as an alternative [14-16]. The penalty function method looks more preferable due to the possibility of solving optimization problems with functionals in which significant nonlinearities are present, and also because of the same applicability to classical and no classical problems. The main disadvantage of the penalty function method is its practical applicability only to problems of small dimension.

In the task of designing a safe reactor, several tens of control parameters and functions are commonly used. The functionals of the problem F_i (u) have a complex dependence on the vector u of control parameters.

Automation of the search for optimal reactor layouts with a large dimension of the problem can be achieved using iterative methods [14, 15]. However, in multi-extreme problems, iterative methods can lead to a relative rather than an absolute optimum. Therefore, it is always useful to repeat the solution of the problem, starting with different values of the control parameters. If in this case the same controls are obtained, then it can be hoped that the iterative search has led to the absolute optimum.

Linear programming methods (in particular, the simplex method) allow solving problems with a large number of control parameters. Practical problems of reactor optimization (with nonlinear functionals) are related to nonlinear programming problems. There are various methods for solving them. The simplest of them is based on the linearization of the problem, that is, the approximation of the nonlinear dependence F_i (u), where i = 0, 1, I, by segments of linear functionals. High accuracy of approximation is ensured by reducing the intervals of dividing by u. After replacing F_i (u) with a piecewise continuous dependence on u, the problem is solved by one of the linear programming methods. The sequential linearization method does not require preliminary transformation and retains the non-classical nature of the problem. This method is implemented in the form of a stepwise process of searching for the optimum, which starts at some point determined by the selected value of the control vector. The change in the values of the controls at each step of the search for the optimum is carried out by solving a linear programming problem formulated using the linearization of the problem functionals.

Consider the problem of linearizing a single objective functional F₀ (u) under constraints in the form of nonstrict inequalities F_i (u) ≤ F_i^*, i = 1, 2,…, I, by the method of successive linearization. This is an iterative method, that is, the solution is found using successive iterations in u. The method is based on lining up a sequence of controls obtained as a result of iterations:  u(1), u(2),…, u(j),… (uk^min ≤ uk ≤ uk^max, k = 1, 2,…, K), which improves (in this case, minimizes) the value of the objective functional.

The transition from iteration to iteration is carried out by choosing the variation δu^(j):

u ^(j+1) = u^(j) +δu^(j), δu^(j) << u ^(j).

The main condition for carrying out iterations is that the constraints

uk^min ≤ (uk ^(j) + δuk ^(j)) ≤ uk^max (where k = 1, 2, …, K)

are satisfied and the conditions

F_i (uk ^(j) + δuk ^(j) ) ≤ F_i *, i = 1, 2, …, I.

The most laborious part of the above-considered optimal search scheme is the linearization of the problem associated with the calculation of the sensitivity factors of the functionals to the control parameters. Their calculation is accompanied by the solution of conjugate equations. The sensitivity factors are calculated using the relations of the theory of small perturbations.

The main disadvantage of the method is the problem of choosing the step of changing the control parameters. With a large step, the linearity of the problem is violated, with a small step, the time for solving the problem increases (i.e., the efficiency of solving the problem decreases). The linear approximation for the approximation of a nonlinear function is valid only for a small neighborhood of the control vector. To eliminate this drawback, two methods are used:

• restriction of the norm of the vector u;
• the penalty for large deviations must be accounted for.

In the second case, the rate of convergence of the method is higher. In this case, instead of the linear programming problem, it is necessary to solve the quadratic programming problem [16].

During the optimization process, additional information appears (about the nature of the change in the safety functional, about the shift of the maximum to the adjacent zone, etc.); therefore, it is desirable to provide for the possibility of user intervention at any stage of research.

2.6. Basic Models for Calculating the Functionals of the Problem. Neutron-physical calculation of the reactor

The calculation begins with the preparation of nuclear data. Data preparation includes several stages [17]:

• Experimental data acquisition;
• Verification of previously unprocessed (“raw”) measurements;
• Comparative assessment of data quality and selection of the most preferred ones;
• Preparation of previously selected data and use in neutron-physical calculation programs;
• Data validation and development of recommendations for their use.

Four nuclear data centers operate under the auspices of the IAEA [13, 18]:

• Nuclear Data Section (Vienna);
• OECD NEA Data Bank (Paris), including the Japanese National Data Center of JAERI;
• Brookhaven Centers (USA and Canada);
• Russian Center (SSC RF – IPPE, Obninsk).

There are data libraries of Western European cooperation JEF (Joint Evaluated File Progect – the modern version of JEFF-3.3 [13, 18], coordinated by the OECD NEA (Economic Cooperation and Development Nuclear Energy Agency) working group. The NEA agency unites 28 countries in Europe, North America and the Asia-Pacific region.

In the calculations of fast reactors (without a moderator), a library of materials important for the technology of fusion reactors, EFF (European Fusion File), is sometimes used. The EAF (European Activation File) library is used to obtain the activation cross-sections. There are complex libraries. For example JEFF-3 includes JEF, EFF, and EAF. Modern versions of the following libraries are often used: JENDL-3.3 (Japanese Evaluated Nuclear Data Library [13], BROND-3.1, ABBN (Russia, State Research Center of the Russian Federation – IPPE) [13] and CENDL-3.2 (China).

All Evaluated Nuclear Data Libraries (files) use the same ENDF / B format (ENDF / B-VII.1 and VIII.0 [13, 18].

In the general case, there are three types (stages) of neutron-physical calculation [17]:

• Calculation at the stage of conceptual development,
• Detailed calculations of the reactor structure,
• Calculations for planning the operation of the reactor must be carried out.

Calculations of the first type (stage) are carried out at the initial design stage, when high accuracy is not required. The purpose of the calculations is to determine the potential advantage of a given type of reactor or the effectiveness of new reactor elements. Research of some innovative projects requires exact knowledge of nuclear constants for new materials in nuclear technology.

The main requirement for calculations of the second type (stage) is high accuracy and calculated demonstration of the safety of the developed reactor. The estimates obtained at the previous step of the calculations are replaced by new estimates, including the reactor kinetics: temperature changes in the reactivity, density and geometry of the core components, including possible changes in power, coolant flow rate, and coolant temperature at the core inlet. At this stage, accurate estimates of fuel enrichment, correct accounting of control rods are required [17].

Calculations of the third type are important for assessing the power and temperatures of each fuel assembly, fuel burnup (change in reactivity), and fuel swelling. On the basis of calculations of neutron fields and fields of γ-quanta, the development of the reactor protection is carried out.

The field of neurons and the effective multiplication factor of neutrons in the Dragon-M code are calculated based on the solution of a multi-group (26 groups by energy) diffusion equation in the approximation of a quasi-critical reactor [19, 20]. It is assumed that the cylindrical reactor consists of several radial and axial zones. The zones are homogeneous, that is, the materials in the zones are mixed. To solve the equation, a semi-direct method of iterative synthesis is used.

The neutron diffusion equation has the form (notation generally accepted in the theory of nuclear reactors: D is the diffusion coefficient, Ф is the neutron flux density, Σ is the macroscopic cross sections, k is the effective multiplication factor etc. [20]:

$$\nabla_r \left[ D_k(r,z) \nabla_r \Phi_k(r,z) \right] + \nabla_z \left[ D_k(r,z) \nabla_z \Phi_k(r,z) \right] -$$

$$- \Sigma_{ad^{(k)}}(r, z)\, \Phi_k(r, z) + \sum_{l=1}^{k} \Sigma_{d^{(l \rightarrow k)}}(r, z)\, \Phi_l(r, z) +$$

$$+ \chi_k / k \sum_{l=1}^{K} \left[ \nu_{f^{(l)}} \Sigma_{f^{(l)}}(r, z) \right] \Phi_l(r, z) = 0.$$

2.7. Calculation of changes in the nuclide composition

It is assumed that the reactor consists of I radial (i = 1, 2,…, I) and J axial (j = 1, 2,…, J) zones. Within each zone (i, j), the properties of the medium are constant. The change in the nuclide composition is modeled by the corresponding equation:

$$d \rho_{i,j,l}(t) = \left[ \int_{0}^{T_{ij}} \rho_{i,j,l}(t)\, dt \right] / T_{ij}.$$

Where ρ_i,j,l (t) is the concentration of the l-th nuclide in the zone (i, j), T_{i, j}  is the campaign of the zone.

The approximation of uniformly partial refueling is used. The diffusion equations and the equation for changing the nuclide composition are solved together iteratively.

2.8. Calculation of the Vorth of Neutrons and the Vorth of Atomic Nuclei

To determine the vorth of neutrons and the vorth of nuclei (conjugate functions of the neutron flux density and concentration of nuclei, respectively), a variation approach is used. The approach assumes the formulation of the Lagrange operator of the neutron field. On the basis of the value functions, the coefficients of sensitivity of the corresponding functionals to the control parameters are determined

2.9. Thermal Hydraulic Calculation

The thermo hydraulic calculation takes into account the release of energy in nuclear reactions of fission of heavy nuclei and capture of neutrons. It is assumed that there is no heat transfer in each zone along the fuel element axis. The average temperatures of the core components are determined through the average volumetric heat release in each design zone.

2.10. Strength Calculation

The strength calculation is carried out according to the method presented in [7].

2.11. Simulation of ATWS

Modeling of emergency modes is based on the joint solution of the equations of point neutron kinetics (six groups of delayed neutrons are used), the unsteady heat equation, the coolant energy equation and the reactivity balance equation [3]. Reactivity coefficients are calculated using the Dragon-M code or can be calculated separately using the WIMS-D5B [21] or MCU-4 [22] code.

When calculating safety functionals, it is necessary to model complex interrelated and independent dynamic processes.

2.12. Refinement of Optimization Results

The diffusion approximation gives significant errors in calculating the void effect of reactivity in a no uniform reactor. For this reason, it is necessary to refine calculations using mathematical models and codes that do not use the diffusion approximation. The most accurate (precision) models are based on solving the gas kinetic equation of neutron transport. There are two main forms of writing this equation:

• gas-kinetic equation of neutron transport – the Boltzmann equation [22, 23],
• integrated equation of neutron transport – Peierls equation [24].

The author has developed hierarchical models with adjustable accuracy based on the MCU-4 precision code [6]. The stationary state of a reactor with a continuous dependence of micro sections on the neutron energy is considered. The model is used to clarify the void and density effects of reactivity and critical parameters of the reactor.

The WIMS-D5B code is used to calculate the temperature and density coefficients of reactivity. Neutrons are grouped into 69 energy groups. S₄-approximation is used.

All the above results are new and obtained by the author personally.

3. Results

3.1.  Research Novelty

The developed software made it possible to obtain new results.

1. On the basis of a systematic approach, a unified methodology for substantiating and analyzing the safety of fast reactors has been proposed and implemented, which includes the following procedures.

• Optimization of the fast reactor core layout was carried out according to a given criterion with restrictions, including restrictions for safety functionals characterizing specified emergency modes or the entire set of emergency modes that are not deterministically excluded. The control parameters include the properties of the core materials.
• an algorithm is proposed for reducing the dimension of the problem of choosing the optimal physical characteristics of the fast reactor core through the following procedures.

a) A procedure for preliminary ranking of emergency situations and their combinations according to the degree of danger (significance for consideration in the problems of optimal design) is proposed. The procedure is based on solving an auxiliary discrete multicriteria problem by the maximin method. The objects of the auxiliary task are emergency modes and their combinations, the criteria are the relative values ​​of the safety functionals, the probability of an accident, etc.

b) An algorithm is proposed to quickly determine the role of reactivity coefficients in complex combinations of emergency modes based on an analysis of the self-protection area.

c) A procedure for the sequential analysis of conflicts of the optimization problem, the use of effective methods of decomposition is proposed.

• An effective procedure for taking into account the uncertainties of scenarios for the development of emergency situations in the problems of optimal design and problems of safety justification is proposed [3, 6]. The author proposed a method for constructing deterministic analogs for solving optimization problems in conditions of uncertainty of scenarios for the development of emergency situations. It is based on a preliminary analysis of the time dependence of safety functional and an analysis of the aggravation and neutralization of emergency situations when they are imposed. Compared with the use of uniformly distributed sequences, the proposed procedure is much more efficient.

2. The following results were obtained for the first time.

• The results of complex optimization of the core layouts of fast reactors with various coolants (silk metals Li, Na, K, Cs and alloys, heavy metals Ga, Pb, Bi and alloys, alloys of alkali and heavy metals) were obtained with restrictions, including for functionals of safety (and in conditions of uncertainty of scenarios for the development of emergency situations).
• The ranking of different coolants of fast reactors according to the degree of preference was carried out. For high-power fast power reactors, the most preferable coolant is based on lead extracted from thorium ores.
• The results of the analysis of the influence of technical systems that determine the time of reducing the flow rate when the pumps are de-energized, the time of transporting the coolant along the primary circuit, etc., on the self-protection of fast reactors were obtained.

3. Reserves of the concepts of BN and BREST reactors of high power in terms of further safety enhancement have been identified.

• For BREST reactors, it is proposed to use a heat transfer agent based on lead and thorium ores (with a high concentration of ²⁰⁸Pb). This contributes to a decrease in the void effect of reactivity and an increase in self-protection against accidents with acceleration on prompt neutrons. It is proposed to use tungsten coatings of the cladding of fuel elements, deposited by means of low-temperature plasma spraying.
• For BN and BREST reactors, it is proposed to use pellet oxide or mononitride fuel based on fine-grained ceramic powder and uranium metal nanopowder. A fuel based on fine-grained powder of UN-PuN (or UN) mononitride and uranium nanopowder is ideal for ensuring the safety of the reactor.

3.2. Practical Relevance of Research

The importance of research is determined by the following factors.

• The Dragon-M code developed and repeatedly modernized by the author allows solving problems of optimal design with constraints, including those characterizing the entire set of emergency situations, in a deterministic setting and in conditions of uncertainty, including the uncertainty of emergency scenarios. Code Dragon-M has no analogues.
• Proposed and implemented procedures for analyzing the uncertainties of scenarios for the development of emergency modes, determining the role of reactivity coefficients in complex combinations of emergency modes (including ATWS), ranking emergency modes according to the degree of hazard, choosing conditionally equally safe (or equally hazardous) reactor assemblies. The results obtained supplement and concretize some sections of the IAEA documents on safety substantiation of nuclear power plants [25].
• The proposed effective hierarchical systems with adjustable accuracy based on well-known high-precision computer codes (MCU) are used to conduct exploratory computational experiments, deterministic substantiation and analysis of safety (void and density reactivity effects), implementation of experimental optimization methods, post-optimization analysis (parameterization). The systems allow you to analyze any type of reactor. To carry out post-optimization analysis and search computational experiments, the author has developed a code for operational modeling of emergency modes of the ATWS type, taking into account their various combinations and the non-simultaneity of the beginning of the processes.
• The parameters that have the greatest impact on the safety of advanced reactor types (including the BREST and BN medium and high power types) were identified, further possible ways to improve their safety were analyzed.
• A systematic comparative analysis of the possibility of using various liquid metal coolants (including unconventional) fast reactors from a wide set of initial data was carried out (alkali metals Li, Na, K, Cs and their alloys, heavy metals Ga, Pb, Bi and their alloys were considered in detail , alloys of alkali and heavy metals). Special attention is paid to alloys with adjustable properties (Na-K-Ca, Pb-Na, Pb-K, etc.). The optimal layouts of reactors with different coolants (obtained with the same formulation of the optimization problem) were compared.
• On the basis of a system analysis, the reserves of the concept of power reactors BN and BREST were identified in order to improve safety.
• the isotopic composition of the lead coolant must be monitored. (The composition of lead recovered even from different samples of the same deposit can vary greatly.) Variations in the concentration of lead isotopes in the coolant have a large impact on neutron balance and safety.

3.3. Selected Results. The Problem of Optimizing the Composition of the Lead Coolant

Research began with the selection of the preferred heat carrier. For this, a multicriteria problem was solved using the lexicographic method. Lead was chosen as the preferred coolant.

Lead contains four stable isotopes (²⁰⁴Pb, ²⁰⁶Pb, ²⁰⁷Pb and ²⁰⁸Pb). The isotopic composition of natural lead is:

1.4% ²⁰⁴Pb – 23.6% ²⁰⁶Pb – 22.6% ²⁰⁷Pb – 52.4% ²⁰⁸Pb.

It was obtained by averaging over all known lead deposits (about 1500). In reality, there are no deposits with such a lead composition in nature. Lead recovered from different deposits has different isotopic compositions. This allows you to optimize the composition of the coolant. Most preferred is lead with a high content of the doubly magic isotope ²⁰⁸Pb. It slows down and absorbs neutrons worse. When used, the void reactivity effect is minimal.

Thus, correction of the solution is possible (optimal coolant). The shifted ideal method was used to select the preferred lead deposit. The author has solved the problem of minimizing the void effect of reactivity. Concentrations of stable lead isotopes were included in the control parameters. The concentration range corresponds to statistical data on the concentrations of different lead isotopes in different deposits.

The scope of determination of lead concentrations is based on the analysis of numerous statistical data on deposits carried out by the author. For example, thorium ores contain lead isotopic composition:

0.01 … 0.076% ²⁰⁴Pb – 0.89 … 26.43% ²⁰⁶Pb –

0.35 … 4.11% ²⁰⁷Pb – 69.15 … 97.74% ²⁰⁸Pb.

Lead and polymetallic ores contain lead isotopic composition:

1.09 … 1.61% ²⁰⁴Pb – 18.64 … 25.17% ²⁰⁶Pb –

21.36 … 30.80% ²⁰⁷Pb – 49.30 … 52.49% ²⁰⁸Pb.

Among the limitations of the optimization room, the restrictions for the security functional simulating the safe termination of ATWS processes and their various (most dangerous) combinations were considered.

It was found that for a BREST-type reactor of infinitely high power (infinite radius of the core); safety is ensured when the ²⁰⁸Pb isotope content is more than 75 … 80%.

3.4.  The Problem of the Optimal Choice of the Fuel Composition

To solve this problem, fuel density, heat transfer capacity and heat capacity were included in the number of control parameters. The criterion of optimality and the constraints of the problem did not change.

Optimal values of density, heat transfer and heat capacity do not allow selection of real fuel material. As a result of the solution, the range of admissible values of these parameters was obtained. This area corresponds to cermets based on a mixture of mononitride micro grains (UN-PuN or UN) and uranium metal nanopowder. For the manufacture of fuel with sealed (obtained) properties, it was necessary to take into account the technological limitations.

The porosity of the ceramic fuel reaches 25%. These pores between micro grains of ceramics can be filled with uranium metal nanopowder. To ensure the safe completion of ATWS processes and their combinations, it is necessary to ensure a nanopowder content of at least 20% (by weight). Complete filling of pores corresponds to a nanopowder fraction of 39%. Thus, the use of these cermets will not only increase the safety of the reactor, but also the power of the reactor (by 39%).

3.5.  The Problem of Optimal Selection of the Fuel Element Cladding Material

To solve this problem, the concentration of alloying additions to structural steel of the AISI 316SS type was included in the number of control parameters [26]. The criterion of optimality and the constraints of the problem did not change.

A wide range of possible additives were considered, including materials not used in nuclear technology. To minimize the void effect of reactivity, the additives were formulated from materials that effectively absorb fast neutrons. To increase the corrosion and erosion resistance, the appropriate materials (primarily tungsten) were included in the additives. To model the coatings, it is necessary to consider the material of the fuel element cladding, consisting of several layers. Each layer is considered separately. The composition of the control vector includes the concentration of materials for each layer of the fuel element cladding.

As a result of solving the problem, a preferred tungsten-coated steel-based material was obtained.

Tungsten coatings are attractive for the following reasons.

• Tungsten coatings minimize the rate of corrosion and erosion of liquid lead construction materials.
• Tungsten coatings exclude the chemical exothermic reaction of chromium and water vapor (analogue of steam-zirconium reaction in thermal reactors). This can be realized when the lead-water heat exchanger tubes are depressurized.
• Tungsten coatings minimize the void reactivity effect.

All the proposed innovations (coolant, fuel, structural materials) were considered comprehensively.

3.6.  Two-criterion Problem of Minimizing the Void Reactivity Effect and Maximizing the Reactor Power (Optimization of the Shape of the Core of a High-Power Reactor)

The author proposed an approach to solving multicriteria continuous optimization problems. It is based on the elements of positional games: sequential decision-making strategies. The approach is implemented on the example of two-criterion optimization (maximizing the power W, minimizing the void effect R of reactivity) of a fast reactor with a lead coolant with restrictions for different functionals, including safety functionals.

The general view of Pareto-optimal solutions to such a problem is shown in Figure 1. Here W^* and R^* are the minimum allowable power value and the maximum allowable value of the void reactivity effect, a – cylindrical core, b – annular and tape core (limitation of void reactivity effect does not prevent an increase in power). The condition R = β (where β is the effective fraction of delayed neutrons) or R = 0 can be considered as a criterion for the limiting level. The disadvantages of using the criterion for the limiting level and the possibility of eliminating them are analyzed.

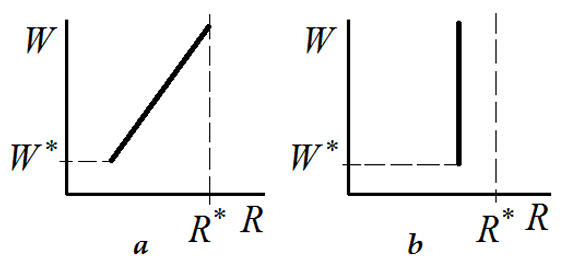
Using the innovative materials (coolant, fuel, and structural materials) discussed above, it is possible to ensure the safety of the BREST-2400 reactor with a traditional (cylindrical) core. The void reactivity effect is negative or much less than β even under the most dangerous scenario of its realization (drainage of the central part of the core). The reactor is safe in ATWS modes and in the most hazardous ATWS combinations.

3.7.  Selection of Parameters that have the Greatest Impact on Safety

The problem was solved by the method of the shifted ideal. Consider a BREST-type reactor of anomalously high power (BREST-2400). The cylindrical core BREST-2400 is assembled from coverless fuel assemblies of the BREST-OD-300 reactor [4] with a square lattice of fuel elements and has three profiling zones.

The parameters w_k that have the greatest impact on safety in LOF WS mode have been identified. The most significant parameter corresponds to | H_i,k | → max;

H_i,k = dF_i / dw_k × w_k/F_i

are the relative coefficients of the sensitivity of the functionals F_i to these parameters w_k. For illustration, three criteria have been selected: H₁ – relative coefficients of sensitivity of the maximum temperature of the fuel element cladding in the central profiling zone in the LOF WS transient mode; H₂ – also, in the mode of natural circulation of the coolant; H₃ – relative sensitivity coefficients of the maximum fuel temperature in the first profiling zone in the LOF WS transient mode.

The most preferable object of the problem of maximizing these three criteria can be considered the most significant from the point of view of the impact on self-protection from an accident of the LOF WS type. Among the parameters wk are effective objects: the average velocity of the lead coolant (object 1), the diameter of the fuel pellet (object 2), the height of the fuel column (3), the relative spacing of the fuel element lattice (4), the volume fraction of the fuel (5), the time of decreasing the consumption (6). Objects 1 through 5 correspond to the center grading area.

Since the critical element of the BREST reactor is the cladding of fuel elements (in emergency modes, there are significant reserves of fuel and coolant temperatures), the most significant criteria are H₁ and H₂. Based on the method of the shifted ideal in coordinates (H₁, H₂), provided that these criteria are equivalent, the objects of the problem can be ranked according to the degree of preference as follows: 4 > 2 > 1 > 3 ~ 5 > 6. (The “>” sign means that the object is more preferable, the sign “~” means the objects are equivalent.)

Similar studies have been carried out for other types of accidents. The self-protection of BREST-2400 against LOF WS accidents is most influenced by the spacing of the fuel rod lattice; from overlapping LOF WS and TOP WS – fuel element lattice spacing and introduced reactivity; from the most dangerous combination (LOF WS + TOP WS + LOHS WS) – introduced reactivity and effective height of the natural circulation circuit.

4. The result of applying the software

The result of using the software is presented in a number of works published earlier by the author (see, for example, [3, 6] and others).

As an example of using the Dragon-M code, consider the problem of minimizing the void effect of reactivity and maximizing the power of a BREST reactor with fuel, coolant, and structural materials traditional for this reactor. Traditional UN-fuel (without uranium nanopowder), which does not contain plutonium, is used as the initial load. Natural lead is used as a coolant. There are no tungsten coatings of fuel rod cladding. The core consists of two zones of different enrichment.

The thermal power of the reactor is 5.680 GW (BREST-2300). The void effect of reactivity during drying of the central part of the reactor is negative and equals minus 1.255. This is not the most dangerous scenario. When bubbles are involved in the core (lead density decreases by 30%), the void reactivity effect is positive and exceeds the effective fraction of delayed neutrons by a factor of 6.

The optimal layout of the BREST reactor is characterized by the following values of the control parameters. Fuel enrichment in the zones is 13.0 and 16.4%, respectively. The diameter of the fuel pellet is the same in both zones and equals 7.42 mm. The relative spacing of the fuel element array is 1.46 and 1.48, respectively. The core height is 110 cm. The radial dimensions of the zones are 178.5 and 50.0 cm, respectively. The mass flow rate of the coolant is 29811 and 30091 kg m^–2 s^–1, respectively.

The following values of the functionals characterizing the emergency modes of ATWS are obtained. The maximum coolant temperature in the LOF WS mode is 1010 and 1022 K, respectively, for two profiling zones. The maximum fuel temperature in TOP WS mode is 1420 and 1560 K, respectively. The steady state power of TOP WS is 13.1% higher than the nominal value.

When the processes LOF WS, TOP WS and OVC WS are superimposed, the maximum coolant temperature is 1062 and 1077 K, respectively.

The reactor cannot be considered safe due to the unacceptably high value of the void reactivity effect.

After the next upgrade of the Dragon-M code, it became possible to consider the properties of materials among the control parameters. In addition, it became possible to consider layered fuel-element cladding. It is not always possible to select materials with desired properties. Permissible density and thermal conductivity corresponds to fuel based on a mixture of ceramics and metal. However, cermets are characterized by a low melting point. The task is to find cermets fuel, the melting point of which is not lower than the melting point of ceramics.

The main result concerns the proposed innovations for fast reactors of high electric power (1.2 … 2.5 GW) with lead coolant. This is a cermet pellet fuel based on a mixture of UN-PuN micro grains (up to 60…80% by weight) and uranium metal nanopowder (up to 20…40%). This is a coolant based on lead extracted from thorium ores. These are tungsten coatings of fuel rod claddings. Taken together, these innovations make it possible to exclude the entire set of accidents (from among ATWS). At the same time, there is no need for passive safety systems provided for in the designs of the BREST reactors [4].

It is assumed that fuel assemblies of the BREST-OD-300 reactor are used in the core [4]. The fuel rod claddings consist of three layers. The inner layer with a thickness of 0.1 mm consists of tungsten. The central layer 0.3 mm thick consists of corrosion-resistant steel of the BREST-OD-300 reactor. The outer layer is 0.1 mm thick and consists of tungsten.

In any combination of ATWS-type emergency modes, the maximum fuel temperatures do not exceed the allowable value (1350 K), the maximum fuel cladding temperatures do not exceed the allowable value (1150 K), there is a large margin for coolant boiling (about 1000 K). The most dangerous scenario for the implementation of the void effect of reactivity is associated with the depressurization of the tubes of the heat exchanger “lead – water vapor of the secondary circuit” and the involvement of bubbles in the central part of the core. The most dangerous decrease in the average density of lead by 30 … 40%. In this case, the void effect of reactivity is negative.

For comparison, in the BREST-OD-300 reactor under construction, it is possible to “pick up” a combination of emergency modes when the operation of passive safety systems is required. Under the most dangerous implementation scenario, the void effect is positive [4]. Calculations using the MCU code show that when the reactor power is increased (project BREST-1200), the void effect of reactivity exceeds the effective fraction of delayed neutrons by about 6 times. This takes the BREST reactor project beyond the concept of “natural safety”.

5. Discussion

The module for modeling ATWS emergency modes and calculating sensitivity coefficients as part of the Dracon-M code was developed by the author taking into account the experience of researching emergency modes accumulated by the world community. These are the published results of experimental modeling of ATWS emergency modes at the EBR-II reactor [5]; results of experiments on BN-600, BOR-60 and “Rapsodie” reactors, FFTF and BFS facilities.

Experimental simulations of ATWS modes are costly and difficult. (Similar experiments were carried out in the USA at the EBR-II reactor in the late 1980s [5]). Comparison of the results of mathematical modeling of ATWS emergency modes in BN-800 and BREST-OD-300 reactors, carried out by the author, with the results of similar studies, confirm the possibility of using the author’s code. For example, the results of modeling the LOF WS mode in BN-800, carried out according to different programs in Germany, France, Japan, Russia, India, predict the beginning of sodium boiling in 16.72 … 18.96 s after the main circulation pumps of the primary circuit are de-energized [27]. Similar calculations carried out by the author give a value of 17 s.

The proposed algorithm, which increases the efficiency of decision-making in the problems of the initial stage of reactor design, is in good agreement with the well-known methods of system analysis (Golubkov’s method [28]), approaches of the theory of decision-making. The author’s approach to taking into account the uncertainties of scenarios for the development of emergency modes is based on the well-known fact that the minimization of subjective interference is possible by obtaining additional information when solving the problem. Such information appears during a preliminary analysis of the possibility of aggravating and neutralizing emergency modes when they are superimposed, carried out using the method of modeling emergency modes.

When carrying out informal procedures, intuitive concepts are used. To combine mathematical theories and informal procedures into a single methodology, it was necessary to formalize intuitive concepts (one of the main tasks of game theory): a conservative approach to calculating security functionals, conditionally equally safe and equally dangerous layouts; when emergency modes are imposed – dominant, competing, equivalent processes, neutralization and aggravation of emergency modes.

The safety of the BREST-OD-300 reactor under construction and the BREST-1200 conceptual design is higher than the requirements of the Russian regulatory and technical documentation (Standard of the State Corporation Rosatom “Basic Rules for Nuclear Safety in the Production, Use, Processing, Storage and Transportation of Nuclear Fissile Materials”, 2016. Federal Norms and rules in the field of the use of atomic energy “General provisions for ensuring the safety of nuclear power plants”, 2015.) The safety of the reactor when using the proposed innovations regarding fuel, coolant and structural materials (coatings of fuel cladding) is even higher. The results obtained supplement and specify some sections of the IAEA documents on NPP safety analysis (for example, the document “Accident Analysis for Nuclear Power Plants. Safety Reports Series no. 23, IAEA, Vienna, 2002”).

Field experiments, similar to those carried out at the EBR-II reactor [5], are practically impossible due to the high risk and cost of such experiments. Separate experiments (including thermal-hydraulic ones) were carried out on the lead loop of the pilot BOR-60 reactor (NIIAR, Dimitrovgrad, Russia). The author did not participate in these experiments.

6. Conclusion

The research carried out is based on a comprehensive and correct use of well-known scientific approaches and methods related to operations research. The studies carried out constitute applications of operations research to solving the problem of ensuring safety at the initial stage of reactor design.

In the research, the computational and optimization complex Dragon-M, which has no analogues, was used. The optimization results can only be compared with the variant calculations carried out by the designers of the new generation reactors. The parameters of the BN-800 reactor core configurations obtained using the Dragon-M complex when solving various optimization problems and tasks without an optimality criterion are in good agreement with the accepted values ​​for BN-800 (including for the version with mononitride fuel [27]). The main difference between the results obtained by the author consists in taking into account the restrictions for the security functionals. In most cases, such restrictions significantly affect the choice of the core layout.

The author proposes and implements an effective procedure for solving problems with constraints for safety functionals under conditions of uncertainty of scenarios for the development of emergency situations, based on obtaining additional information and the possibility of abandoning the use of the traditional approach (criteria of the theory of games for choosing rational decisions).

An algorithm that increases the efficiency of decision-making in the tasks of the initial design stage, substantiation and analysis of the safety of fast reactors was developed and implemented. The proposed and implemented methods, models, approaches and procedures are combined into a single methodology, which is an application of operations research to solving a practical problem associated with the development of new generation reactors.

Optimal design problems with constraints for reliability and safety functionals in a deterministic formulation and under conditions of initial data uncertainty, including the uncertainty of emergency scenarios, as well as practically important auxiliary multicriteria problems were solved.

The solution to the problem of choosing the optimal characteristics of the fast reactor core and particular problems, including the choice of the preferred coolant and others, is based on a systematic approach. Similar tasks of system analysis are solved on the basis of operations research methods.

Elements of operations research (mathematical programming, multicriteria optimization, Markov decision-making models, decision-making procedures under conditions of risk and uncertainty, game theory, etc.) are used to solve the problem of choosing the optimal physical characteristics of a liquid-cooled fast reactor core that satisfies the series given requirements (including self-protection against the entire set of severe accidents, not deterministically excluded).

At the stage of validation of the Dragon-M and FRISS codes, the results were compared with the known results obtained earlier.

The calculation and optimization results for the Dragon-M code were compared with the results obtained for much simpler codes developed much earlier [7]. These codes do not consider functionals that characterize emergency situations. The results of ATWS accident simulations were compared with the full-scale results of experiments conducted in the USA at the EBR-II reactor [5]. A comparison was made of the results of simulation of individual emergency modes with the results of experiments carried out in different countries on fast reactors and stands.

When designing a new generation reactor, the characteristics of emergency modes are not exactly known in advance. For this reason, an analysis of the uncertainties of the initial data was carried out, including an analysis of the uncertainties of scenarios for the development of emergency situations [29]. This procedure includes several steps. At the first stage, the areas of permissible perturbations are determined by reactivity, coolant flow rate, and coolant temperature at the core inlet. (All emergency modes are modeled using a combination of these perturbations.) At the second stage, individual emergency modes from among the ATWS were identified and studied. As uncertain data, the values of the disturbances that initiated the emergency mode, the time of introduction of the disturbance, the law according to which the disturbance is introduced (linear, hyperbolic, and others) were considered. At the next stage, the possibility of neutralizing and aggravating emergency situations when they were imposed was considered. This made it possible to obtain additional data for analysis. These additional data made it possible to abandon the well-known methods for selecting points in the space of uncertain data, in which it is necessary to formulate deterministic analogues (LPτ-sequences, the max-min principle). As a result, a more efficient procedure for choosing points at which it is necessary to formulate deterministic analogs has been obtained. In addition, the number of points was reduced by approximately 10 times with the same accuracy [29].

The decision-making model in such a problem has such a large dimension and a large number of internal connections that it complicates the possibility of its practical implementation. A rationalization of the decision-making procedure was required, connected, first of all, with an increase in its efficiency in the presence of heterogeneous and uncertain information. The developed software makes it possible to design new generation reactors, in which accidents with unacceptable releases of radioactive substances outside the nuclear power plant are excluded.

The problem is considered on the example of one of the types of nuclear reactors of the new generation. The ideas are quite applicable to the study of industrial facilities that pose an increased danger.

Conflict of Interest

The author declared no conflict of interest.

1. IRENA, Renewable capacity statistics 2021, Abu Dhabi, International Renewable Energy Agency, 2021. https://www.irena.org/publications/2021/March/Renewable-Capacity-Statistics-2021
2. BP Statistical Review of World Energy 2021, 70th edition, London: Whitehouse Associates, 2021, https://www.bp.com/content/dam/bp/business-sites/en/global/corporate/pdfs/energy-economics/statistical-review/bp-stats-review-2021-full-report.pdf
3. V.S. Okunev, “Designing of new generation of the тuclear reactors“, AIP Conference Proceedings, vol. 2195, pp. 020012, 2019, https://doi.org/10.1063/1.5140112
4. V.V. Lemekhov, A.V. Moiseev, M.K. Sarkulov, V.S. Smirnov, O.A. Yarmolenko, Yu.V. Lemekhov, Yu.S. Cherepnin, V.P. Vasyukhno, D.A. Afremov, “Present-day status and development prospects of fast-neutron lead-cooled reactors“, 5th Int. scientific and technical conf. Innovative design and technologies of nuclear power (ISTC NIKIET-2018), ISTC NIKIET, Moscow, pp. 35 –37, 2018.
5. Nuclear Engineering and Design, vol. 101, no. 1, pp. 3–91, 1987, https://www.sciencedirect.com/journal/nuclear-engineering-and-design/vol/101/issue/1
6. V.S. Okunev, “System analysis methodology for decision making in the design problems of new generation nuclear reactors“, J. Phys.: Conf. Ser. , vol. 2001, pp. 012005, 2021, doi:10.1088/1742-6596/2001/1/012005
7. N.I. Geraskin, A.M. Kuzmin, A.A. Kashutin, A.V. Kobiak, D.V. Morin, A.E. Novikov, V.S. Okunev, M.O. Shvedov, V.V. Khromov, “Complex optimization of the fast reactors“, Proc. of International Conference on the Physics of Reactors (PHYSOR-90), Marseille, Fr., vol. 4, 1990.
8. M. Zeleny, The theory of the displaced ideal multiple criteria Decision Making. Kyoto. Springer-Verlag, New York, 1976.
9. R. Steuer, Multiple criteria optimization: theory, Computation and application, Wiley, New York-Chichester-Brisbane-Toronto-Singapore, 1986.
10. P.L. Yu, Multiple criteria decision making:cConcepts, techniques, and extensions, Plenum Press, New York-London, 1985.
11. IAEA Publucation. https://www.iaea.org/publications, last accessed 2021/12/23.
12. IAEA-TECDOC-1531. Fast reactor database 2006 Update, IAEA, Vienna, 2006, https://www-pub.iaea.org/MTCD/Publications/PDF/te_1531_web.pdf
13. IAEA: Evaluated nuclear data file (ENDF). Database Version of 2021-05-14. Vienna, IAEA, 2021, https://www-nds.iaea.org/exfor/endf.htm
14. B. Bunday, Basic optimisation methods, London, Edward Arnold, 1984.
15. M. Minoux, Mathematical programming: theory and algorithms, Wiley, 1986.
16. D.M. Himmelblau, Applied nonlinear programming, McGraw-Hill., 1972.
17. IAEA-TECDOC-1083: Status of liquid metal cooled fast reactor technology, Vienna, IAEA, 1999.
18. IAEA: Nuclear Data Servises, Vienna, IAEA, 2018, https://www-nds.iaea.org/public/download-endf/
19. H. Sekimoto, Nuclear reactor theory. COE-INES Textbook. Tokyo Institute of Technology, 2007, http://www.nr.titech.ac.jp/coe21/events/pdf/NuclReactorTheoryTextbook.pdf
20. M.L. Adams, Introduction to nuclear reactor theory, Texas A&M University, Galveston, 2009.
21. WIMSD-IAEA Library, IAEA, Nuclear data services, 2014, https://www.iaea.org/resources/databases/wimsd-iaea-library
22. E.A. Gomin, ”MCU-4 status”, Questions of atomic science and technology, Series: Physics of nuclear reactors, vol. 1, pp. 6–32, 2006.
23. J.F. Briesmeister (Ed.), MCNP — a general Monte Carlo N-particle transportcCode. Version 4B, LA-12625, Manual, 1997.
24. WIMS-D/4. EnergysScience and technology software center: NEA Data Bank, United Kingdom Atomic Energy Authority. Reactor Group, General Reactor Physics Division. Atomic Energy Establishment. Winfrith, Dorchester. Dorset, 1967.
25. Accident analysis fornNuclear power plants: safety reports Series no. 23, IAEA, Vienna, 2002.
26. E. Oberg, F.D. Jones, H.L. Horton, H.H. Ryffel, Machinery’s handbook (29th Edition). C.J. McCauley (ed.). Industrial Press, New York, 2012.
27. IAEA-TECDOC-1139: Transient and accident analysis of a BN-800 type LMFR with near zero void effect, IAEA, Vienna, 2000.
28. G.V. Gokubkov, M.G. Gokubkov, M.I. Manzhelii, I.V. Karpov, Optical quantum properties od GPS signal propagation medium-D layer. In Bychkov V.L., Gokubkov G.V., Nikitin A.I. (eds.) The atmosphere and ionosphere. Elementary Processes, monitoring, snd ball lightning, pp. 1–69. Springer International Publishing, Sweetzerland, 2014.
29. V.S. Okunev, “An effective method for accounting for the uncertainty of scenarios for the development of emergency situations in nuclear reactors”, IOP Conf. Ser.: Earth Environ. Sci., vol. 979, pp. 012106, 2022, doi:10.1088/1755-1315/979/1/012106

Citations by Dimensions

Citations by PlumX

Crossref Citations

This paper is currently not cited.

No. of Downloads per Month

No. of Downloads per Country