The article considers the issue of modeling the multi-step process of customs clearance of goods in foreign trade. A mathematical model of control of the process under consideration has been developed. A brief review of existing methods for solving the linear programming problem with variable coefficients of the target function is given. The essence of customs risks has been studied and a method for identifying customs risks of reliability using threshold matrixes has been proposed. An algorithm for controlling the reliability of the customs value of goods is developed and the results of the implementation of this algorithm are given

1. Introduction

International trade has long been considered the fundamental form of international economic relations. The pace of globalization in the first quarter of the XXI century confirms the role of international trade as the main driver of socio-economic development of countries. Analysis of the dynamics of international trade in the period from 2000 to 2015 shows that the export of developed countries increased from $4.243212 trillion to $8.613816 trillion (+103.00%), developing countries – from $2.059532 trillion to $7.344534 trillion (+256, 61%), countries with economies in transition – from 149.573 billion dollars to 525.571 billion dollars (+251.38%). On average, the volume of exports of world trade goods increased by 254.2% [1].

At the same time, the customs services of the countries participating in international trade play an important role in the international supply chain. There is a theory in the scientific literature, according to which any customs system successively passes several separate phases of its activity, characterized by the specificity of its relations both with foreign trade participants and with the state. Today, the customs systems of developed countries are in the “customs for foreign trade participants” phase, while for most developing countries the “customs for the government” phase is characteristic, and in a number of disadvantaged and underdeveloped countries, the “customs for themselves” phase is observed. [2].

Conversely, the faster a country’s customs service approaches the “customs for foreign trade participants” phase of development, the faster the country approaches the level of developed countries. Today, the development of the activities of the customs service of each country is possible only through the use of modern information and communication technologies. Therefore, such requirements are imposed to the methods of customs service management as orientation of models on artificial intelligence, possibility of synthesis of adaptive control system and application to complex analysis of multilevel system.

From this point of view, the task of optimal management of the process of organizing customs control and customs clearance of non-trading goods is relevant.

2. The problem of optimal management of the customs clearance process

The purpose of any type of control is to change the state of the control object in accordance with a predetermined task. Control methods should answer the question, “how can we construct an algorithm that can control a given object in a way that achieves a predetermined goal?”. To do this, the developer needs to know how the control object will respond to different influences, that is, the control object model is needed.

There are many definitions to the concept of “model”. One of them is close to our question: “A model is an object that allows you to study the behavior of another object, which is called the original”. The model and the original should be similar so that the conclusions drawn from studying the model can be applied to the original[3].

As noted above, in order to study the control object, it is necessary to know how it reacts to various influences on it. If we denote these influences as “input” signals for the control object, then the changes occurring under the influence of these “input” signals can be regarded as “output” signals. That is, the object interacts with the external environment using “incoming” and “outgoing” signals.

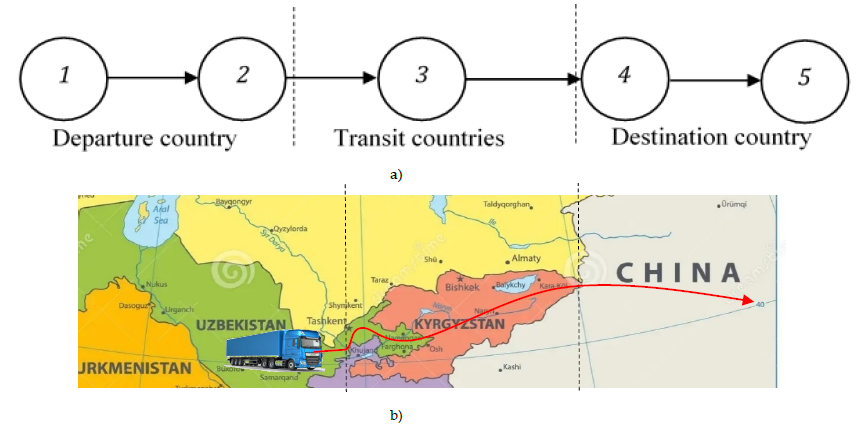
If the documents submitted to the customs authorities in this process are taken as “inputs” for modeling the multi-stage customs clearance process and denote them by X(t), then customs clearance will be carried out in accordance with these documents. In this case, you can take as an “output” signal the information received as a result of customs clearance, and designate it Y (t) (Fig. 1.)

here:

c(t), r(t), v(t)- set of impacts of customs clearance results to management;

c(t) – objects of organization of customs control (goods, vehicles, persons), documents, additional information flows, etc.;

r(t) – risks that may affect the process (information, human, financial and other resources);

v(t) – obstacles to achieving the goal (refusal, etc.).

This set of influences moves the customs clearance system Z(t) towards a given goal and generates a vector of output results Y(t). From a mathematical point of view, the function Y(t) is the reaction of the control object – the customs clearance process – to external influences.

Optimal management of the multi-stage customs clearance process can be carried out with respect to a number of objectives. In  particular, optimization is envisaged in relation to one of the following goals:

• ensuring the completeness of revenues to the state budget, i.e. maximization of revenues to the state budget;
• minimize the amount of arrears that may not go to the state budget, that is, possible damage to the budget;
• Reduction of expenses of the entrepreneur – participant of foreign trade, i.e. minimization of damage caused to him in the process of customs clearance;
• minimize time for customs clearance processes;
• other purposes.

The purpose of this study is the optimal management of the customs clearance process, as well as minimizing the time spent on this process. Because it will ultimately lead to minimization of time for the customs clearance process, as well as to maximize revenues to the state budget and minimize the costs of the entrepreneur – participant of foreign trade.

It is known that in the general case the question of linear optimization can be expressed as follows [4]:

$$\max(\min) \, f(x) = \sum_{k=1}^{n} c_k x_k \tag{1.1}$$

$$\left.\begin{array}{ll}
\sum_{k=1}^{n} a_{jk} x_k = b_j, & \text{if} \quad j = \overline{1, m_1} \\
\sum_{k=1}^{n} a_{jk} x_k \geq b_j, & \text{if} \quad j = m_1+1, \, m_2 \\
\sum_{k=1}^{n} a_{jk} x_k \leq b_j, & \text{if} \quad j = m_2+1, \, m \\
x_k \geq 0, & k = \overline{1, n}
\end{array}\right\} \tag{1.2}$$

In this research paper, in the formation of a mathematical model of optimal control of the process of multi-stage customs clearance in relation to the time consumed, it is proposed to use the stages of customs clearance shown in Table 1.

Table 1. “Customs Clearance Process: Task Execution Matrix”

The presented list of functions is grouped into four main blocks. These functions are performed by customs authorities, foreign trade participants and enterprises providing services in the customs field. The organization of customs clearance is characterized by a large number of operations performed, the complexity of which is determined by a combination of factors: type of goods, country of origin, declared customs value of the goods,

From the above table it follows that the process of multi-stage customs clearance covers 18 stages, of which stages 1-7 are performed by a foreign trade participant or a customs broker, stage 8 – by a cargo carrier, stages 9-11 – stages are performed by owners of customs warehouses, and for execution 12 – 18 – the stages are responsible for the employees of the customs service. That is, in formula (1.1), n = 18.

$$f(t) = \sum_{k=1}^{18} r_k t_k \rightarrow \min \tag{1.3}$$

where: r_k = r_k (X) – the level of risk of execution of the k-stage; X=X(x₁,x₂,…,x₅₈) –vector, x_i  elements of which are determined depending on the value of the corresponding columns of the cargo customs declaration. In practice, the level of risk of customs clearance is determined depending on the documents submitted for customs clearance, including the cargo customs declaration.

At the same time, the estimated time of duration of the customs clearance process for responsible executors is determined by normative and directive documents, in particular, documents approved by the Cabinet of

Ministers of the Republic of Uzbekistan.  If we denote them as b₁, b₂, b₃ and b₄, respectively, conditions (1.2) will come to the following form:

$$\left.\begin{array}{ll}
0 < \sum_{k=1}^{n} a_{jk} t_k \leq b_1;\ a_{jk} = 1 & \text{if } j = \overline{1,m_1} \\
0 < \sum_{k=1}^{n} a_{jk} t_k \leq b_2;\ a_{jk} = 1 & \text{if } j = \overline{m_1+1,m_2} \\
0 < \sum_{k=1}^{n} a_{jk} t_k \leq b_3;\ a_{jk} = 1 & \text{if } j = \overline{m_2+1,m_3} \\
0 < \sum_{k=1}^{n} a_{jk} t_k \leq b_4;\ a_{jk} = 1 & \text{if } j = \overline{m_3+1,m_4} \\
t_k \geq 0,\ k = \overline{1,n}
\end{array} \right\} \tag{1.4}$$

here: n=18, m₁=7, m₂=8, m₃=11, m₃=18.

a_jk=0 at the values of index j, which are not included in conditions (1.4)

The above formulas (1.3) and (1.4) give a mathematical model of the problem of optimal control of the process of multi-stage customs clearance.

3. Analysis of existing methods for solving the linear programming problem with variable coefficients

The obtained results (1.3) and (1.4) show that the mathematical model of the problem of optimal control of the process of multistage customs clearance has the form of a linear programming problem with variable coefficients of the objective function. Currently, there are a number of effective methods available for solving the linear programming problem.

In particular, for constant values of the coefficients (r_k) of the objective function (1.3) under the limiting conditions (1.4), a number of methods are used in practice to determine its minimum value. These include methods such as the simplex method, the deployment of a function on algebraic polynomials, Fourier series, the use of spline functions, and others. A sufficient number of computer programs for numerical solution of this problem have been implemented.

However, the features of the problem of optimal control of the multi-stage customs clearance process, which is described in (1.3) – (1.4) are variable coefficients of the target function. The functions r_k = r_k(X) which represent the degree of risk of the k – process, is a function of the variables of the cargo customs declaration. This requires a specific approach to solve this problem.

In particular, the 3rd and 4th stages “calculation of the customs value of goods” and “calculation of the amounts of customs payments” of Table 1. are important stages in the customs clearance process in ensuring the fulfillment of fiscal tasks assigned to the customs authorities.

This fact indicates the relevance of improving mathematical modeling of the customs clearance process and its comprehensive study.

At the same time, the study of scientific papers on the study of similar problems showed that a sufficient number of studies have been carried out and certain methods have been developed for solving the problem of linear programming with variable coefficients.

For example, the work of [6] is one of the relatively early studies in this area. The problem of parametric programming of the following form is considered:

$$\left.\begin{array}{l}
f(X) = \sum_{j=1}^{n} c_j x_j,\quad X = \{x_j\},\quad c_j \in \mathfrak{S} \\
\sum_{k=1}^{n} a_{ij} x_j = b_i;\quad i = \overline{1,m} \\
x_j \geq 0,\ j = \overline{1,n}
\end{array} \right\} \tag{2.1}$$

here: c_j – elements of some ordered functional prospace ℑ, a_ij, b_i – known, a x_j – unknown real numbers, X – plan of the problem (non-negative solution of the problem (2.1)) Plan X* is optimal if for any plan X f(X)<f(X*). Note that the values of the target function (2.1) belong to the space ℑ , in which the usual properties of numerical inequalities are known to hold.

The existence of a solution to problem (2.1) is proved in this paper by introducing the concept of resolving combinations of problem (2.1), considered as elements of the space ℑ , are comparable with the zero of this space, i.e., if x∈R, then one and only one of three relations holds: x>0, x <0, and x =0. Under these conditions, the following theorem is proved:

Theorem. The problem (2.1) with a non-empty set of plans and a target function bounded from above, satisfying the condition: all solving combinations of coefficients of the target function are comparable to zero, has a solution.

However, the paper does not provide a methodology for determining the existing solution.

In [7], a parametric programming problem of the following kind is considered:

$$\left.\begin{array}{l}
\min(\max)\ z(x) = \sum_{j=1}^{n} c_j(x) x_j \\
\sum_{j=1}^{n} a_{ij}(x) x_j \geq b_j(x), \quad i = \overline{1,m}
\end{array} \right\} \tag{2.2}$$

here a_ij( x), b_i( x) and c_j( x) – some piecewise constant argument functions x = (x₁, x₂ , …, x_n ).

The functions a_ij( x), b_i( x) and c_j( x) are defined on the same set G = {x ∈ G ⊂ R_n }. There exists a finite partition G = UG_k , (k =1, l) such that the functions are constant in each subset G_k, and G_k and G_k+1  can intersect only along their boundaries.

By requiring that in problem (1)-(2) the target function z(x) and the constraint functions:

$$f_i(x) = \sum_{j=1}^{n} a_{ij}(x)x_j – b_j(x), \quad i = \overline{1,m}$$

be continuous and convex, by a simple enumeration of a finite number of regions G_k, in each the usual linear programming problem is solved.

The work [8] is devoted to the study of the problem of parametric programming of the following form:  

here: X=(x₁,…x_n)^T – n-dimensional vector of unknown variables, which satisfies the constraints (2.3), forming the set of admissible solutions of the proble;

$$\left\{ \begin{aligned}
&f(X) = c_1(t)x_1 + c_2(t)x_2 + \ldots + c_n(t)x_n \xrightarrow[x \in D]{} extr \\
&A(t)X \leq b(t) \\
&x_j \geq 0,\ j = \overline{1,n}
\end{aligned} \right.\tag{2.3}$$

b(t)=(b₁(t),b₂(t),…,b_m(t))^T and C(t)=(c₁(t),…,c_n(t))^T – parametric vectors of free terms of constraints and coefficients of the target function, respectively;

A(t)_n×m=(a_ij(t)), i=1…n, j=1… m is an n×m-dimensional matrix of parametric constraint coefficients. The functional dependence on the parameter t can be either linear or nonlinear.

In the work on the basis of simplex method and differential transformations the methods of solving linear programming problems with parametric coefficients of the target function and right parts of constraints are considered, allowing to organize simple iterative calculations and excluding the solution of systems of inequalities.

$$\left\{ \begin{aligned}
&\max F = \max \sum_{j=1}^{n} c_j x_j \\
&\sum_{j=1}^{n} a_{ij} x_j \left\{ \begin{array}{c} \leq \\ = \\ \geq \end{array} \right\} b_j,\quad i = \overline{1,m} \\
&x_j \geq 0,\quad j = \overline{1,n}
\end{aligned} \right.\tag{2.4}$$

In this case, it is assumed that the parametric functions X=(x₁,…x_n)^T, b(t)=(b₁(t),b₂(t),…,b_m(t))^T and C(t)=(c₁(t),…,c_n(t))^T are sufficiently smooth, have smooth differentials, and have explicit expressions.

In the studies of the authors [9] and [10] the linear programming problem with variable parameters is considered, in which not only variables included in its composition, but also coefficients, as well as the right part and parameters (coefficients at variables) of the target function can change.

An approach is proposed that allows solving linear programming problems with interdependent variable coefficients using the simplex method.

The formulation of the problem is as follows:

here: 𝑚 — number of restrictions,

𝑛 — number of variables,

and additional restrictions on variable coefficients:

$$\left\{ \begin{aligned}
&a_{ij}^- \leq f_{ij} a_{ij} \leq a_{ij}^+ \\
&s_k^- \leq \sum_{i=1}^{m} d_{kj} a_{ij} \leq s_k^+,\quad k = \overline{1,K} \\
&\sum_{i=1}^{m} p_{lj} a_{ij} = r_l,\quad l = \overline{1,L} \\
&c_j^- \leq f_j c_j \leq c_j^+
\end{aligned} \right.\tag{2.5}$$

In the constraint system (2.4)-(2.5), all parameters ⁻_𝑖𝑗, 𝑎⁺_𝑖𝑗, 𝑠⁻_𝑘, 𝑑_𝑘𝑖𝑗, 𝑠⁺_𝑘, 𝑝_𝑙𝑖𝑗, 𝑟_𝑙, 𝑐⁻_𝑗, 𝑐^+𝑗, f_𝑖𝑗 are constants set during the problem formulation process. Conditions (2.5) are sometimes called interval conditions and problem (2.4) is an interval linear programming problem with interdependent variable coefficients.

Under these conditions, the following lemma is proved by constructive method:

Lemma. Let in the linear programming problem (2.4) – (2.5) there are variable coefficients that depend on a parameter of the form a_ij=a_ij(t_j), having a domain of definition on a certain interval [α_j; β_j] and continuously differentiable on it. Then the simplex method applied to solve such a problem converges if the above constraints are satisfied.

The proof is constructive in the sense that it substantiates the execution of all stages of the implementation of the simplex method, taking into account condition (2.5). The essence of the proposed method is that at each step the number of the column entering the basis at the next iteration of the simplex method algorithm is determined and calculations are performed on the points of minimum of the function 𝑎_𝑖𝑗(t) In [11], the following parametric programming problem was considered:

$$\left\{ \begin{aligned}
&\sum_{i=1}^{n} c_i x_i + c_0 \leq Z, \\
&\sum_{k=1}^{n} a_{ik} x_k \leq b_i,\quad i = \overline{1,m} \\
&x_j \geq 0,\quad j = \overline{1,n} \\
&Z_{\min} – ?,\quad x_i(Z_{\min}) – ?
\end{aligned} \right.\tag{2.6}$$

To solve the linear parametric programming problem, it is assumed that the coefficients change insignificantly with respect to their average values, as, for example, the cost of goods depending on the exchange rate or inflation rate. In such cases, when the relative changes in the coefficients are of the order of 10% or less, it is proposed to use the asymptotic perturbation method. Its essence is reduced to the search for the decomposition of the desired functions into functional series, the rapidity of convergence of which depends on the “smallness parameter” of the relative change of the functions affecting the problem.

The algorithm for solving the problem is as follows. We assume solutions of the problem (2.6) in the form of series consisting of corrections of the corresponding order:

Z = Z⁰ + Z¹ + Z² +…;

x_i = x_i⁰ + x_i¹ + x_i² +…;

The values of Z^k and x_i^k are determined in an iterative way, assuming Z⁰ and x_i⁰ as the first approximation in the iteration process. The values of Z⁰ and x_i⁰are the solution of a simple linear programming problem (1), when their average values a_ij⁰, b_i⁰ and c_j⁰ are taken instead of the variable coefficients a_ij(x), b_i(x) and c_j(x).

For example, if c_j(x) is continuous in the interval [0;1], then we take as its mean value:

$$c_j^0 = \int_0^1 c_j(x)\,dx\tag{2.7}$$

The above brief overview shows that the problem of linear programming with variable coefficients is a well-known problem that has sufficient applications and is being studied everywhere. A certain number of methods for solving this problem have been developed, which are successfully applied depending on the problem formulation and application area.

4.  Trigger graph model of the process and customs risk criterion

Based on the results of the above analysis, we can say that all methods of solving the linear programming problem with variable coefficients imply certain requirements for the ratio of the coefficients of the target function. First, an explicit form and smoothness of the parametric function are required. Second, when applying some methods of solving this problem, additional conditions such as continuity and differentiability of the given function are required.

However, in the case of the problem of optimal control of the customs clearance process, the parametric coefficients of the target function do not have an explicit expression and the above conditions cannot be required. Consequently, there are certain difficulties in applying the available methods to solve the problem, and it is required to explore new approaches.

Based on the latter findings, to minimize the target function (1.3) under conditions (1.4), it is proposed to ensure minimization of the coefficients of the target function r_k(X), which represent the degree of risk of the k – process. Without violating the conditions of the stated problem and generality, we can assume that:

$$r_k(X) \geq 0,\quad k=\overline{1,18}\tag{3.1}

The task of minimizing the coefficients of the target function r_k(X) gives rise to the task of investigating the essence of customs risks

The above studies have led to the fact that customs risks from the mathematical point of view is a function of many variables, is not presented in an explicit form, there are considerable uncertainties in its characteristics in terms of smoothness, continuity, differentiability and other qualities.

Before moving on to research on the specifics of the customs risk, it is important to consider the essence of the risk as a whole, since it is inherent in various fields of activity. There are many approaches to defining the concept of “customs risk“. For example, the working group of the World Customs Organization, preparing the document “World Customs Organization Compendium on Customs Risk Management” in 2011, gave the following definition: “Risk: the result of doubts arising in relation to objects” [12]. In scientific literature it is defined as follows: “Risk is the probability of violation of customs legislation associated with evasion of payment of customs duties and taxes due” [13].

In these or other definitions of customs risk, which are observed in previously published scientific papers, the “probability of violation of customs legislation” passes as the  main predicate. This means that the mathematical  expression of customs risk must necessarily include the “probability of violation of customs legislation” model.

Based on the above, in order to develop a mathematical approach to this definition, it is necessary to study customs legislation both  at  the  national  level  and  at  the

international level. At the same time, the importance of studying international conventions in the field of customs should be emphasized, as the process of a foreign trade operation is directly related to foreign partners.

Fig. 2. shows a simplified graph model (a) and an explanatory scheme (b) of the process of foreign trade operations.

An analysis of the customs legislation on the day of the present research shows the following. By the beginning of the second half of 2023, more than 2216 normative legal documents related to the regulation of the activities of customs authorities of the Republic of Uzbekistan were in force (Table 2).

Table 2: Information on legal documents related to the regulation of the activities of the customs authorities of the Republic of Uzbekistan

(author’s development)

Despite the fact that there is such an extensive customs legal framework, the main task of the customs authorities of the Republic of Uzbekistan is to protect the economic security of the country and almost all the rules of this framework are focused on the following two main tasks [14]:

1. fulfillment of the fiscal task – ensuring the completeness of customs payments collection;
2. prevention, detection and suppression of violations of customs legislation, including smuggling.

The study of customs legislation and practical experiments showed that between the above-mentioned main tasks of managing foreign trade operations, in terms of procedure, there is an irreconcilable contradiction. This contradiction is manifested in the following:

• the key parameter for increasing customs payments is the time spent on customs clearance of foreign trade goods: the less time spent on customs clearance of a particular foreign trade cargo, the more cargo will be cleared for a certain period of time, hence, more customs payments will be made to the state budget during this period. At the same time, the number of violations of customs legislation and the volume of goods of illegal circulation are increasing, since the time for a detailed study of the consignment of goods being processed remains minimal.
• the key parameter for reducing customs law violations is also the time spent on customs clearance of foreign trade goods: the more time to study a specific consignment of foreign trade cargo, the less chance there is to commit violations of customs legislation.

At the same time, the amount of revenues to the state budget from customs payments decreases, as the foreign trade turnover for a certain period of time decreases.

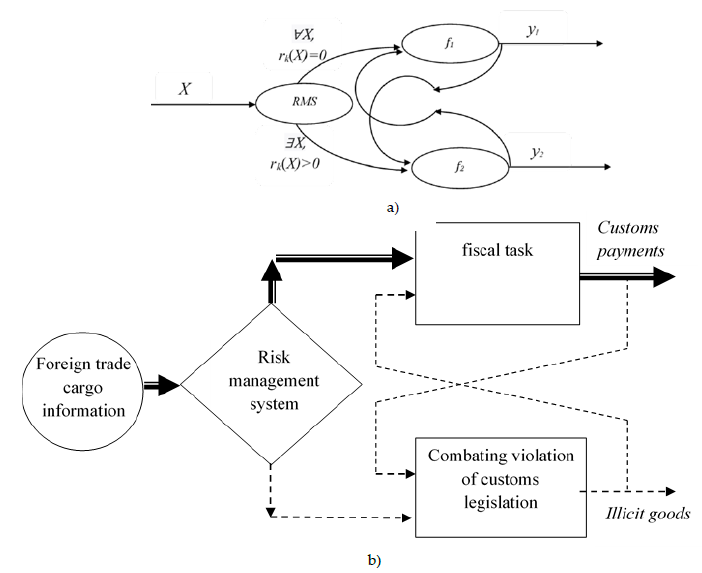
To minimize irreconcilable contradictions between the main tasks of managing foreign trade operations in procedural terms, in practice, a customs risk management system is used. Trigger graph model of the main tasks of foreign trade operations management with application of risk management system is shown in Fig.3.

It should be noted that both functions – the function y₁, which reflects the volume of receipt of customs payments, and the function y₂, which reflects the volume of illegal goods (customs law violations) are functions of time, i.e. y_i= y_i(t). Both functions are inversely proportional to the ratio of customs clearance time, i.e.

$$y_i = \varphi_i\left(\frac{1}{t}\right),\quad \text{where } \varphi_i\text{ — linear functions},\quad i=1,2\tag{3.2}$$

On the other hand, the conducted experiments showed that with an increase in the volume of goods of illegal circulation (offenses of the customs legislation), the receipts of customs payments decrease, i.e. functions y₁ and y₂ are inversely proportional to each other:

$$y_1 = \psi_i\left(\frac{1}{y_2}\right),\quad \text{where } \Psi_i\text{ — linear function}\tag{3.3}$$

The mathematical contradiction reflected in (3.2) and (3.3) gives rise to the need for an optimization problem about the choice of time for customs clearance of foreign trade goods. It is required for each batch of goods to review the duration of customs clearance time and choose it so that there would be maximum receipt of customs payments and minimum volume of goods of illegal turnover (violations of customs legislation).

This task can be solved only if the following conditions are met:

1. choose the minimum time for customs clearance, in the absence of customs risk;
2. choose the time of customs clearance sufficient to ensure the minimization of the customs risk, if it is detected.

5. Risk assessment of the reliability of customs information

We mentioned above that in the scientific literature there is a theory according to which any customs system successively goes through several separate phases of its activity, characterized by the specifics of its relations both with foreign trade participants and with the state. Three phases of development are noted: the customs systems of developed countries are in the “customs for foreign trade participants” phase, in most developing countries the phase “customs for the government” is characteristic, and in a number of underdeveloped countries there is a “customs for themselves” phase.

Proceeding from the fact that the Republic of Uzbekistan is carrying out large-scale works on transferring the customs service to the phase “customs for foreign trade participants”, the authors of this paper study customs risks, categorizing them into three classes:

• customs risks for business;
• customs risks of economic security;
• corruption risks.

a) when it comes to the customs risk for business, it means the submission of an unreliable customs declaration by the business to the customs authorities. Analysis of the database of violations of customs legislation for several years shows that every 4th fact about such violation is the result of false declaration.

Despite the fact that at the present stage of development of foreign trade, favorable conditions are created for a law-abiding participant in foreign trade, the laws react rather harshly towards them if they have submitted an unreliable customs declaration to the customs authorities. The consequence of such phenomena for them can sometimes be undesirable, severe and long-lasting.

Therefore, the primary task of the customs service of the Republic of Uzbekistan today is to minimize customs risks for business.

b) the customs risk of economic security is the probability of violation of customs legislation by a participant in foreign trade, associated with evasion of payment of due customs duties and taxes.

c) corruption risks shall mean abuse of official powers, receiving and giving bribes, bribery, mediation in bribery, commercial bribery or other illegal use by a customs officer of his/her official position contrary to the legitimate interests of the state, in order to obtain benefits for himself/herself or for third parties.

Thus, the first step in solving the problem of optimal management of the customs clearance process (1.3) – (1.4) is to minimize the implicit function r_k(X), which represent the degree of risk of unreliable declaration of foreign trade goods, i.e. minimization of customs risks for business. To solve this problem it is necessary to assess the reliability of information about the goods on all its parameters, i.e. it is required to conduct a multivariate analysis of information about the goods. Information about the goods is fully reflected in the cargo customs declaration.

The research of the authors of this paper has shown that the customs cargo declaration is one of the fundamental documents of the customs clearance process. It is formalized in the form of a multidimensional matrix X, which is the source of state customs statistics [15].

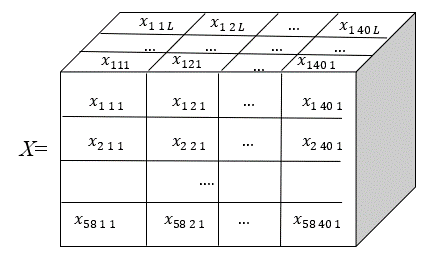
A brief characterization of the customs cargo declaration is as follows:

1. number of columns – 58;
2. the level of detail of each column of the cargo customs declaration is determined depending on the complexity of the task, but not more than 40;
3. L – the total number of cargo customs declaration per year.

It should be noted that each layer of this matrix corresponding to l=l₀ reflects a separate cargo customs declaration. It can be labeled as follows:

$$X_0 = \begin{pmatrix} x_{11|0} & x_{12|0} & \cdots & x_{140|0} \\ x_{21|0} & x_{22|0} & \cdots & x_{240|0} \\ \vdots & \ddots & \ddots & \vdots \\ x_{581|0} & x_{582|0} & \cdots & x_{5840|0} \end{pmatrix}\tag{4.2}$$

Assessing the validity of information about the goods for all its parameters requires controlling and assessing the validity of all elements of the matrix (4.2). The study of existing methods for solving this problem showed that the problem of identifying unreliable customs declarations is a special case of the general and, as you know, ancient problem of identifying false information, i.e. how to distinguish “truth” from “falsehood”.

This famous problem is mentioned in many ancient writings, beginning with Aristotle (384 BC), who is the founder of logic as a science [16]. One of the great scientists who devoted his entire conscious life to the study of the task of distinguishing “truth” from “falsehood” is Imam al-Bukhari. His book Al-Jami’as-Sahih has been tested for over 11 centuries and is considered the most authentic book today [17].

The concept of information reliability has different meanings in philosophy, the theory of forensic evidence, epistemology, logic, probability theory, psychology, natural science and other areas. There is no single definition of the term, although many famous philosophers have tried to give their own definition of the term. In logic and philosophy, reliability often acts as a synonym for the concept of “truth” and characterizes indisputable, firmly substantiated and demonstrative knowledge.

A “threshold matrix” (TM) is proposed to determine the concept of reliability of the elements of the customs cargo declaration (4.2.) (4.3.).

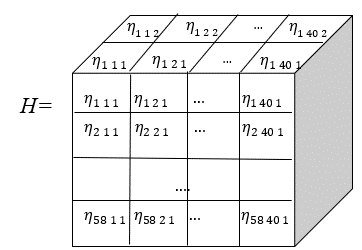
here: – some positive real numbers or textual information.

Definition 1. Each element of the matrix is called reliable if the following condition is satisfied

$$\eta_{j1} \leq x_{ji|0} \leq \eta_{j2}\tag{4.4}$$

where: 1≤ i ≤58, 1≤ j≤ 40.

Definition 2: If all elements of the matrix  are reliable, then the customs cargo declaration is called reliable.

Conditions (4.4) are called criteria, and the elements of the “Threshold Matrix” are called indicators of the reliability of the cargo customs declaration.

From Definition 1-2, the following statement is easily proved:

Statement 1. If at least one element of the matrix does not satisfy the conditions (4.4), then the corresponding cargo customs declaration is unreliable.

To assess the reliability of a cargo customs declaration, the authors of this work propose the following function:

$$\rho_{ij} = \left\{ \begin{array}{ll}
e^{\eta_{j1} – x_{ji|0}}, & \text{if } \eta_{j1} \geq x_{ji|0} \\
1, & \text{if } \eta_{j1} \leq x_{ji|0} \leq \eta_{j2} \\
e^{x_{ji|0} – \eta_{j2}}, & \text{if } x_{ji|0} \geq \eta_{j2}
\end{array} \right.\tag{4.5}$$

here:1≤ i ≤58, 1≤ j ≤40.

The function  can be estimated as follows: when the conditions  are satisfied for all 1≤ i ≤58, 1≤ j ≤40 function value ; otherwise, – . In other words, the function  reflects the quantitative assessment of the reliability of the element   X₀ of the cargo customs declaration. Then the matrix ρ (4.6) is the matrix of the reliability of the cargo customs declaration X₀.

$$\rho = \begin{pmatrix}
\rho_{11} & \rho_{12} & \cdots & \rho_{1\,40} \\
\rho_{21} & \rho_{22} & \cdots & \rho_{2\,40} \\
\vdots & \vdots & \ddots & \vdots \\
\rho_{38\,1} & \rho_{38\,2} & \cdots & \rho_{38\,40}
\end{pmatrix}\tag{4.6}$$

with the above notations, the following theorem is proved:

Theorem 1. In order for the cargo customs declaration X₀ to be reliable, it is necessary and sufficient to fulfill the following condition:

$$\mathbf{P} = \prod_{i=1}^{58} \prod_{j=1}^{4} \rho_{ij} = 1\tag{4.7}$$

Ρ is the coefficient of reliability of the customs cargo declaration X₀. It follows from (4.5) and (4.7) that the coefficient Ρ takes on the values Ρ=1 only if for all 1≤ i ≤58, 1≤ j ≤40 the conditions are satisfied, otherwise Ρ >1.

6. Algorithm of control of risks of reliability of calculation of customs payments

To verify the above results, let’s consider the tasks of controlling the risks of reliability of the calculation of customs payments. The amount of customs payments for the import of goods is determined as follows:

S=D+E+V

where: D- the amount of customs duty, E- the amount of excise tax, V- the amount of value-added tax on goods. They are determined mainly by the so-called “ad valorem rates”. This means that the amount of each of the above types of customs payments is determined depending on the established rate in percentage terms. For example, the rate of value added tax in the Republic of Uzbekistan is set at 12% of the customs value of the goods.

The formulas for calculating them are as follows:

D = d c;

E = ec;

V= 0.12 (c +D +E).

where: c is the customs value of the goods, d is the rate of customs duty, e is the rate of excise tax.

After simple arithmetic transformations, you can get: S=D+E+V= c (d+ e+0.12(1 + d + e)).

Hence, it can be seen that the amount of customs duties on imports of a particular good depends directly on the customs value of the good c. The lower the customs value of the goods, the lower the receipt of customs payments to the state budget.

Considering this circumstance, the “Threshold Matrices” were formed in the form of “Price Information Bulletins“. The table reflects the following data:

η₇– date of registration of the customs value of goods;

η₃₃– commodity code in accordance with the Harmonised System (HS);

η₁₅ – code of the country of departure of the goods;

η₃₄ – country of origin code;

η₄₅– customs value of goods.

The other elements of the “threshold matrix” for the considered criterion of the reliability of the customs value of goods are of little importance.

Then conditions (4.4) have the following form:

$$|\eta_7 – x_7| \leq 90,$$

$$\eta_{15} = x_{15},$$

$$\eta_{33} = x_{33},$$

$$\eta_{34} = x_{34},$$

$$\eta_{45} \leq x_{45}$$

Taking into account the above designations, an algorithm for controlling the customs value of goods has been developed (Fig. 4)

It should be noted that the “Price Information Bulletin” is a characteristic feature of the national legislation of the Republic of Uzbekistan, and is not observed in the practice of the customs services of other countries.

7. Conclusion

In conclusion, I would like to note that the authors of this article conducted research on minimizing customs risks for business. This is due to the fact that large-scale work is being carried out in the Republic of Uzbekistan to organize the work of the customs service on the principle of “customs for participants in foreign trade”. Because, the faster the country’s customs service approaches the stage of development “customs for foreign trade participants,” the faster the country approaches the level of developed countries.

When it comes to customs risk for a business, it means submitting an unreliable customs declaration to the customs authorities on the part of the business. An analysis of violations of customs legislation over several years shows that every 4th fact of such a violation is the result of an unreliable declaration. It is known that for an unreliable declaration, punishment is provided up to criminal. The consequences of such an incident can sometimes be undesirable, severe and long-term for business.

The research carried out within the framework of this article showed that the task of identifying unreliable customs declarations is a special case of the general and, as we know, ancient task of identifying false information, i.e. how to distinguish “truth” from “falsehood”.

To determine the reliability of a cargo customs declaration, the authors proposed a “threshold value matrix” method, which in fact forms a “knowledge base” of a production expert system that represents knowledge in the form of “IF-THEN” rules. The block diagram of the algorithm for one of these rules is shown above in Fig. 4.

The software of this expert system determines existing errors in the customs cargo declaration as they are received by the customs authorities via the Internet and automatically informs the foreign trade participant about this. No administrative or criminal sanctions will be applied to a foreign trade participant who promptly and voluntarily corrects errors.

Currently, 53 logical rules have been established in the knowledge base to control the reliability of the customs value of goods, which make it possible to localize such customs risks. As a result of the implementation of these rules in 2022, in 88 thousand 897 cases, the risks of “unreliability of the customs value of goods” and debts to the state budget in the equivalent of more than 9 million 968.8 thousand US dollars were prevented.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

We thank the editor of the Journal of Engineering Research and Sciences and the anonymous reviewers for their valuable comments. All errors and omissions remain the responsibility of the authors.

1. A. O. Rudneva, “International trade: specifics and prospects of participation of developed, developing and transition countries,” MIR (Modernization. Innovation. Development), vol. 8, no. 3, pp. 430-438, 2017, doi: 10.18184/2079–4665.2017.8.3.
2. A.D. Ershov, “Formation of customs services in foreign economic activity,” Scientific notes of the St. Petersburg branch of the Russian Customs Academy, no. 1(23), pp. 174-192, 2005.
3. S.V. Zvonarev, “Fundamentals of mathematical modeling: textbook,” Yekaterinburg: Ural University Press, 112 p., 2019.
4. R.I. Ibyatov, “Optimization methods in problems of mathematical modeling,” methodological guidelines, Kazan: Kazan State Agrarian University Publishing House, 32 p., 2016.
5. R. V. Fedorenko, “Methodology of management of service complexes in the customs sphere,” Dissertation for the degree of Doctor of Economics, Samara, 2015. https://www.sseu.ru/wp-content/uploads/2015/06/Dissertatsiya-Fedorenko-R.V.pdf. (dissertation in Russian with an abstract in English)
6. A.G. Pinsker, “A linear programming problem with variable coefficients of the purpose function,” Sib Math J, vol. 20, pp. 466–468, 1979, doi: 10.1007/BF00969958. (article in Russian with an abstract in English)
7. M. O. Gavrilova, “On problems of linear programming with piecewise constant coefficients,” Scientific journal “Bulletin of the Perm State Technical University. Chemical technology and biotechnology”, Perm, No. 9, pp. 172-179, 2010.
8. A. G. Avetisyan, L. S. Gyulzadyan, “A method for solving problems of parametric linear programming based on differential transformations,” Scientific journal “Izvestia of the Tomsk Polytechnic University”, vol. 324, No. 2, pp. 25-30, 2014.
9. D.A. Salimonenko, “A method for solving a linear programming problem with variable coefficients in the form of parametric functions,” Scientific journal “Vestnik of the Bashkir University”, Ufa, vol. 20, No. 1, pp. 25–29, 2015.
10. D.A. Salimonenko, A.M. Ziganshin, V.A. Mudrov, Yu.D. Salimonenko, “On interdependent variable coefficients in linear programming problems,” Scientific journal “Mathematical Structures and Modeling”, Omsk, No. 2 (58), pp. 96–111, 2021, doi: 10.24147/2222-8772.2021.2.96-111.
11. S.P. Kravchuk, I.S. Kravchuk, O.V. Tatarnikov, E.V. Shved, “Perturbation method for solving linear programming problems with a parameter,” Scientific journal “Fundamental Research”, Moscow, No. 5, pp.299-303, 2015.
12. WCO, “Customs Risk Management Compendium,” Brussels, Belgium, June 2011, http://www.wcoomd.org. 
13. S.E. Tamrazyan, “Customs Risks: Essence, Management and Evaluation,” Scientific journal “Economics and Management in the XXI century: development trends”, No. 23, pp.168-172, 2015.
14. A.A. Saidov, F.A. Khakimova, T.T. Abdurakhmonov, “The concept and model of the ‘soft component’ of the risk management system of customs authorities,” Scientific journal “Bulletin of the Russian Customs Academy”, Moscow (Russia), No. 3, pp. 100-109, 2022, doi: 10.54048/20727240 _2022_03_100 (article in Russian with an abstract in English).
15. A.A. Saidov, “Classical Methods of Controlling the Reliability of Information and Features of Their Application to Customs,” Monograph, Tashkent, 498 p., 2021. (monograph in Russian with an abstract in English)
16. Aristotle, “Metaphysics,” Translation from Greek by P. D. Pervov and V. V. Rozanov, Moscow: Institute of Philosophy, Theology and History of St, Thomas, 232 p., 2006.
17. Muhammad ibn Ismail al-Bukhari, “Al-Jami’ as-sahih,” Translation by Vladimir (Abdullah) Nirsha, Moscow (Russia), Umma Publishing House, 448 p., 2017.

Citations by Dimensions

Citations by PlumX

Crossref Citations

No related articles were found.