My Firsttt Heading

Automated grading systems can help save a lot of time when evaluating students’ assignments. In this paper we present our ongoing work for a model for generating correctness levels. We utilize this model to demonstrate how we can grade students SQL queries employing partial grading in order to allocate points to parts of the queries well written and to enable provision of feedback for the missing parts. Furthermore, we show how we can grade the queries taking into account the skill level of students at different stages of SQL learning process. We divide the stages into introductory, intermediary, and advanced stages and in each apply different type of grading that takes account the students’ knowledge at that stage. We implemented this model in our class and graded 5 quizzes containing more than 25 different questions for 309 students. We discuss 3 examples for each stage and offer comprehensive examples of the model in action.

1. Introduction 

Partial grading in SQL software exercises is awarding a selected portion or a fraction of a whole grade. It involves giving points to parts whereby the student has done well or deducting points to parts missed. An advantage of partial grading is that we are able to acknowledge students’ efforts by awarding points to the correct parts of a query. This helps in protecting their motivation to learn [1]. Furthermore, we are able to pinpoint the parts of a query the student has missed. This helps in providing constructive feedback to help the student improve on their work. Partial grading systems which are able to carry out this form of grading have been extensively researched [2, 3, 4, 5]. Nevertheless, these systems do not address different skill levels of students at various stages of the learning process. We propose a model in which students’ skill levels are taken into consideration. We refer to this as dynamic grading.

There are three types of knowledge acquired by students in programming courses, syntactic, conceptual, and strategic [6]. In our project, we broadly classify these groups of knowledge into 2 types, syntactic and semantic [7, 8] as it makes it manageable to translate our grading model into a running program. Students learn well when taught syntax and semantic knowledge in parallel while syntax knowledge develops as a result on repetition [8]. Even though this is the case, novice students might struggle more with syntax during the introductory lessons than at the end [9]. Various methods have been proposed of how to teach SQL in various steps. Some research proposes teaching SQL in an increasing order of difficulty [10]. This order begins from teaching ’SELECT’ syntax to recursive SQL at the end. Other research proposes teaching SQL in a series of steps

involving building a query one clause at a time [11]. The first clause would be SELECT followed by FROM clause then WHERE clause and so on. A mental model in which learners learn SQL starting with remembering SQL concepts followed by comprehending the concepts with creating the queries at the end have been proposed as well [12]. In the various learning styles proposed, students are novice during the start of the class struggling with syntax and at the end have accumulated enough knowledge to write completely semantically correct queries. We considered to utilize these findings to grading as well. To this effect, our goals in this paper are to demonstrate how we can:

• Assign a discrete level that shows how correct a query is, in relation to an instructor’s specifications.
• Factor in students’ knowledge level when calculating grades.

Also, to demonstrate whether:

• It is possible for an automated grading tool to match the grades given by manual graders.
• If students consider an automated grading tool to be

In this context, a fair grade is a grade that matches the one that would be given by an instructor. Furthermore, this grading capability should be applied consistently to other answers as well.

To factor in students’ knowledge level, we divided a full programming course’s time into three stages. introductory stage, intermediate stage, and the advanced stage. We used syntax, semantics, and results as features for evaluation. For each stage, these three features which we refer to as properties were evaluated in parallel while varying their individual weight to the whole grade. At the introductory stage, syntax had more weight. Similarly, at the intermediate stage, semantics had more weight than the other properties and at the advanced stage, results had more weight.

To carry out partial grading, we used software correctness levels and to enable dynamic grading, we used varying weights for properties like syntax which addressed different skills levels as we will see in this paper. We graded more than 25 different SQL questions for 309 students using different configurations of dynamic grading and we shall discuss 3 of these questions.

1.1. Advantages of skill based grading

Grading students’ work while considering whether they are novice or more advanced can have several advantages. This is in comparison with grading the work of students who are struggling with the new programming language and those who are already familiar with or mastered it the same way.

1. Personalization and Grading students work while considering whether they are novice or advanced would be considered as a personalized and differentiated way. In this manner, novice students are not penalized for not meeting a higher standard as expected of the more advanced students.
2. Student motivation and engagement. By basing the grading on the student knowledge level, their motivation to continue learning and engaging would be protected. This is because, the students are able to view learning the new programming language as something within their capability.
3. Targeted feedback. Due to the differences between novice students and advanced ones, specific feedback can be constructed that caters to the differing needs of Novice students may be more interested in the language syntactic elements while advanced students being more interested in semantic elements.

2. Related work

Partial grading systems have enabled awarding partial points instead of strict 0 or 1 [2, 3, 4, 5]. Some systems are even capable of generating datasets for testing [13]. The limitation of these systems is that they employ inflexible strategies to grade the queries. Our model is able to dynamically grade queries based on the gradual learning process of students. Furthermore, it has the flexibility of adding or removing properties during grading depending on the goals of the instructor.

Correctness levels have been used before to grade SQL queries. Some research has used 8 different correctness levels to partially grade queries [14]. Specifically, Dekeyser et al. [14] use syntax, schema, results, and peer review to grade the queries whereby each code feature is evaluated as either correct or not. Of these 8 levels, 5 are automatically awarded by the system while the rest require manual input. Our model automatically awards 9 different levels using syntax, semantics, and results, evaluating each feature using three categories instead of two. Our model also allows more levels by having the flexibility of adding more properties and their outcomes.

Dynamic grading has been used in other areas apart from SQL. For example, in gradual programming whereby the students learn a programming language in well-defined steps instead of learning everything at once [15].

Binary grading offers only two possible outcomes: correct and incorrect, which does not consider partial correct- ness or incorrectness [16]. As a result, students may not receive points for partially correct submissions. Providing detailed feedback on the areas where students’ understanding is lacking becomes impossible as well. This limitation of binary grading gives rise to the need for partial grading. Our model offers more possible outcomes to enable differentiation of errors.

There are differences between novice and expert programmers. As a result, various research has been proposed which highlights these differences. It has been proposed that expert programmers memorize source code better than novice programmers [17]. In the proposal, the researchers also argued that novices tend to memorize syntactic elements while expert programmers focus on the algorithm. Expert programmers can solve a problem by abstracting the algorithm while novices cannot [18]. As the expertise increases, novice programmers gradually shift from focusing on syntactic elements to the semantic ones [19]. This may indicate that novice programmers are more focused on the language syntax while experts focus on the semantics. Differences among novices and experts have been argued in other fields as well. For example, in physics, it has been proposed that experts might use abstraction to solve a problem while novices use the problem’s literal features [20]. Naturally, computer science students as programmers might show this phenomenon. Even though they may not become full experts in the programming language during the course of the class, they are able to achieve competency [21]. Due to the differences between novice and advanced students, it has been proposed to make the introductory material simple and systematically expand as students’ expertise increases [22]. For example, beginning with writing syntax, comprehending templates, writing code with templates and tracing [23]. Therefore, we considered and utilized these findings to implement our grading model in such a way that it can acknowledge and accommodate these differences.

Grading students work based on unit testing has also been used in other programming languages like Java [24, 25]. Unit testing [26] involves testing the smallest unit in a pro- gram or code that can be isolated. In most cases, the testing parameters are already known by the developers and the testers before runtime. Our syntax analysis is a form of unit testing whereby a student’s query’s syntax is verified based on the target SQL standard and other similar syntactically correct queries. However, neither the testing parameters for our semantic nor results analysis are known up until runtime whereby the system loads the model query and the student query. Also, it is challenging to exactly anticipate the correct semantics since queries written in different ways can have the same meaning. Furthermore, the binary nature of unit testing makes it difficult to carry out partial grading. This means that, our unit tests have additional requirements compared to ordinary unit tests.

3. Software correctness levels

Software correctness in software exercises is the degree to which code written by students satisfy the specifications given by the instructor [27]. Software correctness levels describe this degree [28]. Software correctness in SQL is tested using various techniques. The most used is executing the query and checking the results [29, 30].

There are various properties that can be evaluated to check for code correctness. Some of these properties are: syntax, semantics, results, efficiency, style and performance. During this evaluation, we classify a property into various categories that describe the correctness of the property. In this research, we call such categories outcomes. Examples of outcomes are fully correct, meaning the property completely satisfies the specifications and fully incorrect for otherwise.

Using these properties and their outcomes, we can create a matrix of all the outcomes arranged in such a way that the first row describes the lowest adherence of the properties to the specifications. The last row would describe the complete adherence of these properties to the given specifications. We show such matrices as tables: Table 1, Table 2 and Table 3. The number of properties and outcomes to use de- pends on the grading goals and the programming language. Database managements systems feature query optimizations therefore in SQL we would not evaluate properties like efficiency [31]. In C++, style, complexity and efficiency have been used to evaluate students’ code [32, 33, 34]. In this implementation we focus on three properties: syntax, semantics, and results. for these properties, we evaluate them into three outcomes: correct, minor incorrect( small mistakes like misspells of 2 characters and less) and incorrect. The meaning behind each outcome will be discussed in the method section.

3.1. Property weight

Teaching SQL in a computer science class is done in various stages [10]. One of the most important stages is teaching proper SQL syntax. In this stage, students are introduced to SQL, how it is written, the tools used and how to run commands. Another notable stage is using already learned SQL commands to carry out simple tasks. In this stage students learn how to take simple specifications and turn them into SQL commands that accomplish the given task. Various stages of learning have various goals. Naturally, this should translate to grading goals. Our goal is to modify how grading is done based on the learning stage.

Grading modification is enabled in our model by assign- ing different weights for the properties. For example, At the introductory stage, grading would weigh more on syntax. During the intermediate stage, grading would weigh more on semantics, as the instructor turns their attention to carry- ing out given tasks. Similarly, at an advanced stage, grading would weigh more on results.

3.1.1.Introductory stage grading

At the introductory stage, the instructor would focus on correct syntax. For a student to successfully pass this stage, they would need to be able to write well-formed SQL clauses with correct keywords. For any quizzes at this stage, the instructor would classify the student queries based on how well written the syntax was. At one extreme of this classification, there would be completely incorrect syntax and at the other end fully correct syntax. The instructor would then put a threshold for passing, whereby, students below this threshold would have to practice more on syntax. A 9-magnitude model weighing more on syntax is shown in Table 1. In this model, the instructor might put the threshold for passing at correctness level 6. Students who can pass this threshold would be able to write queries that can be parsed and well executed by the database management system. Even though in this stage we focus on correct SQL syntax, the other properties, semantics and results still matter.

Table 1: Syntax has the most weight, next semantics and then results. inc. refers to incorrect.

3.1.2. Intermediate stage grading

At an intermediate stage, the instructor would turn the students’ attention to solving some tasks. At this point the students already know how to write correct SQL grammar. The instructor would teach how to turn given specifications into correct SQL queries that accomplish the task. For any given quiz at this stage, the instructor would want to check if the students are able to carry out some tasks using SQL. This would involve checking if the students’ queries have the correct semantics. A 9-magnitude model focusing more on semantics is given in Table 2. In this model, the instructor might put a passing threshold at correctness level 6. This means that students with queries below this threshold might be struggling with how to turn some specifications into a semantically correct query.

3.1.3. Advanced stage grading

In the last stage, the students should already have mastered how to write correct SQL grammar. Furthermore, they should be able to turn given specifications into semantically correct SQL statements. At this point, the instructor might focus on making sure the students are able to write queries that return the expected results. This means, grading would weigh more on results. A 9-magnitude model weighing more on results is shown in Table 3. Similarly, as the other stages, the instructor might put the threshold for passing at correctness level 6. Correct semantics imply correct results. Nevertheless, instead of focusing on semantics only, we check results because they give extra information about those queries without fully correct semantics. For example, if the reference correct query output is a subset of a student query, it means the student query may not have carried out correct filtering of results in the WHERE clause.

Table 2: Semantics has the most weight, next syntax and then results. inc. refers to incorrect.

Table 3: Results has the most weight, next semantics and then syntax. inc. refers to incorrect.

The instructor is free to use any threshold for passing that aligns with their goals. Notice how in all the different weights models, the students are still allowed to make minor mistakes without severe points reduction in their grades. This gives appreciation to their efforts in carrying out the tasks.

3.2. Grading

The final grade awarded to a query is calculated using the correctness level assigned as shown below:

$$g = \frac{l – \min(l)}{\max(l) – \min(l)}$$

where g is the grade in the range 0 to 1, l is the correctness level, min(l) is the minimum correctness level and max(l) is the maximum correctness level of a specific model in use. The grade is linearly distributed along the possible correctness levels. This is an improvement to the earlier model which factored in the missing or impossible levels when calculating the grade [28].

3.3. Flexibility in adding or removing properties

Our software correctness model is made up of combinations of the chosen properties and their possible outcomes. The 9-magnitude model shown in Table 1, Table 2 and Table 3 comprises of properties results, semantics and syntax each with 3 possible outcomes: correct, minor incorrect and in- correct. This gives rise to 27 possible combinations of which 9 are usable in our implementation. Unusable combinations are for example, when both syntax and semantics are fully incorrect while the results, fully correct. The instructor is free to choose whichever properties or outcomes align with their teaching goals. For example, they can choose to carry out binary grading using only the results. In this case, property results would have 2 possible outcomes: correct and incorrect. This would translate in the correctness model having 2 levels: level 1 for an incorrect query and level 2 for a correct query. Using the same property, they might opt for a 3 magnitude correctness levels model. In this case, results would have 3 outcomes: fully correct, minor incorrect for results not filtered, i.e. correct results would be contained inside the query results and fully incorrect. Similarly, the instructor can choose syntax and semantics, or results and syntax with various outcomes.

As we see here, the number of properties or outcomes used to construct a correctness model for grading is not fixed. The instructor can add or remove properties and their outcomes as well. Adding properties or outcomes increases the size of the correctness model. This increases the number of correctness levels as well, which translates to higher grading sensitivity. On the other hand, using fewer properties or outcomes reduces the size of the correctness model. This reduces the number of correctness levels, which translates to lower grading sensitivity. In this paper, we demonstrate the power of a correctness model using 3 properties and 3 outcomes. Using 4 properties or outcomes and more or less is also possible in this model.

4. Grading process

Algorithm 1 shows the main algorithm for grading students queries using the correctness model discussed above. This was implemented in C++ under Linux with DuckDB [35] as the database management system.

4.1. Initialization

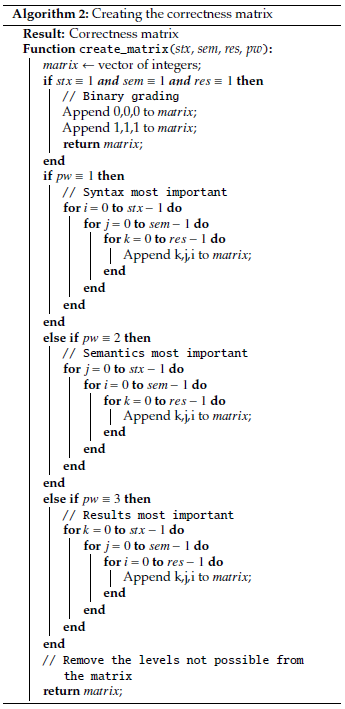
We begin by initializing parameters that will be used to instantiate the correctness model. This involves initializing the number of syntax, semantics and results outcomes that will be used on grading. We also initialize the ’property weight’ variable. We assert that these variables are initialized to integers greater than 0 and a maximum of 3. This maximum is not fixed but can change by adding more properties or outcomes. A correctness model matrix is constructed using this initialization as shown in algorithm 2. This is a 2-dimensional array containing all the various combinations of the properties and their We then remove unusable rows from the matrix.

Algorithm 1: Main Algorithm

Result: Grades

stx ← number of syntax outcomes;

sem ← number of semantics outcomes;

res ← number of results outcomes;

pw ← property weight;

// Ensure 1 ≤ stx ≤ 3, 1 ≤ sem ≤ 3, 1 ≤ res ≤ 3,

1 ≤ pw ≤ 3

text_ed ← 3; // text edit distance tree_ed ← 2; // tree edit distance incorrect ← 0;

minor incorrect ← 1; correct ← 2;

// See Algorithm 2

correctness_m ← create_matrix(stx, sem, res, pw);

// Put reference queries into data

structure

re f ← reference queries;

// Load student queries student ← student queries; for n ∈ {re f } do

n.AS T ← reference query abstract syntax tree;

// Run the query in DuckDB

n.Output ← query result;

end

for n ∈ {student} do if n ≡ {} then

// Empty

n.PARS EABLE ← false;

n.S YN ← incorrect;

else

Parse the query;

if  parseable  then n.PARS EABLE ← true; n.AS T ←

student query abstract syntax tree;

n.Output ← query result;

end else

n.PARS EABLE ← false;

n.S YN ← incorrect;

end end

end

foreach n ∈ {student} do

// See Algorithm 3

syntax_analysis(n, text_ed, syn);

// See Algorithm 4, ref(1) denotes the first query

results_analysis(n, ref(1), res);

// See Algorithm 6

semantics_analysis(n, re f , student, tree_ed, sem);

end

foreach n ∈ {student} do

// See Algorithm 5

get_correctness_level(n, correctness_m, stx, sem, res);

get_grade(n);

end

4.2. Pre-processing

Next, we carry out pre-processing of reference and student queries. For reference queries, we create abstract syntax trees for each and execute them, saving the output in a 2-dimensional array. We used the library, pg_query [36] to create abstract syntax trees. Student queries undergo the same procedure but first, we check if they are parseable. If a query is not parseable, we mark its syntax outcome as incorrect. Then, we carry out syntax, results and semantics analysis finalizing by calculating the correctness level for each query and the subsequent grade. These steps will be discussed next.

4.3. Syntax analysis

Syntax analysis is done first. Algorithm 3 shows how syntax analysis is accomplished. In this stage, all parseable queries are marked as having correct syntax. Next, we check how far the unparseable queries are from being parseable. To accomplish this, we carry out a comparison between un- parseable queries with those that are parseable using text edit distance metric [37]. The parseable queries include both parseable reference and student queries. For those student queries with mistakes of 2 characters and below, we mark as having minor incorrect syntax and edit them. This enables further processing of the queries. For unparseable queries without close reference or correct student queries, we then check the SQL keywords in the query. We employ the same edit distance metric to check how much malformed the keywords are. We identify the SQL keywords using information from the parse tree.

4.4. Result analysis

Result analysis is done next. Algorithm 4 shows how results analysis is accomplished. In this stage, we compare the results of each student query with the results of the reference queries. If both outputs match, the student query is deemed as having correct results. For those queries with different output, we then check if the reference query output is a subset of the student query output. If so, we mark the student query as having minor incorrect results. The rest of cases are marked as having fully incorrect results.

4.5. Semantics analysis

The final analysis involves semantics. Algorithm 6 shows how semantics analysis is accomplished. In this stage we check if the student queries have the intended meaning. First, we mark as having correct semantics, those queries that had correct results in the previous step. Next, we mark unparseable queries as having fully incorrect semantics. This is because in this implementation we cannot verify the severity of the mistakes.

For the rest, we carry out parse tree edit distance comparisons using Shasha Zhang’s algorithm [38]. This is accomplished by comparing parse trees of the student queries under processing and the reference queries together with the student queries with correct output. We further check the text edit distance for those queries found to have a tree edit distance of 1. If this text edit distance is 2 characters or less, the query is marked as containing minor incorrect semantics. The rest of the cases are marked as having fully incorrect semantics.

At this point, the student queries have been tagged with various outcomes for the properties. The outcomes of each query are compared with the outcomes in the correctness matrix. The correctness level of a query is the level with matching outcomes. The grades are calculated in the range 0 to 1, using Equation 1.

Algorithm 6: Semantics analysis

Result: Semantic outcomes

Function

semantic_analysis(query, re f , student, tree_ed, sem): if query.RES ≡ correct then

query.S EM ← correct;

end else

if query.PARS EABLE ≡ false then

query.S EM ← incorrect;

end else

smallest ← 0;

ted ← 0;

foreach m ∈ {re f } do

dist ←

query.AS T and m.AS T distance ;

l_ted ←

query.QUERY and m.QUERY distance ;

if dist ≤ smallest and l_ted ≤ ted then

smallest ← dist; ted ← l_ted;

end end

foreach s ∈ {student} do

if s.RES ≡ correct then

dist ←

query.AS T and s.AS T distance ;

l_ted ←

query.QUERY and s.QUERY distance;

if dist < smallest and l_ted ≤ ted

then

smallest ← dist; ted ← l_ted;

end end

end

if smallest < tree_ed and ted < text_ed

then

if sem ≡ 3 then

query.S EM ← minor incorrect;

end else

query.S EM ← incorrect;

end

query.RES ← correct;

end else

query.S EM ← incorrect;

end

end end

5. Implementation and findings

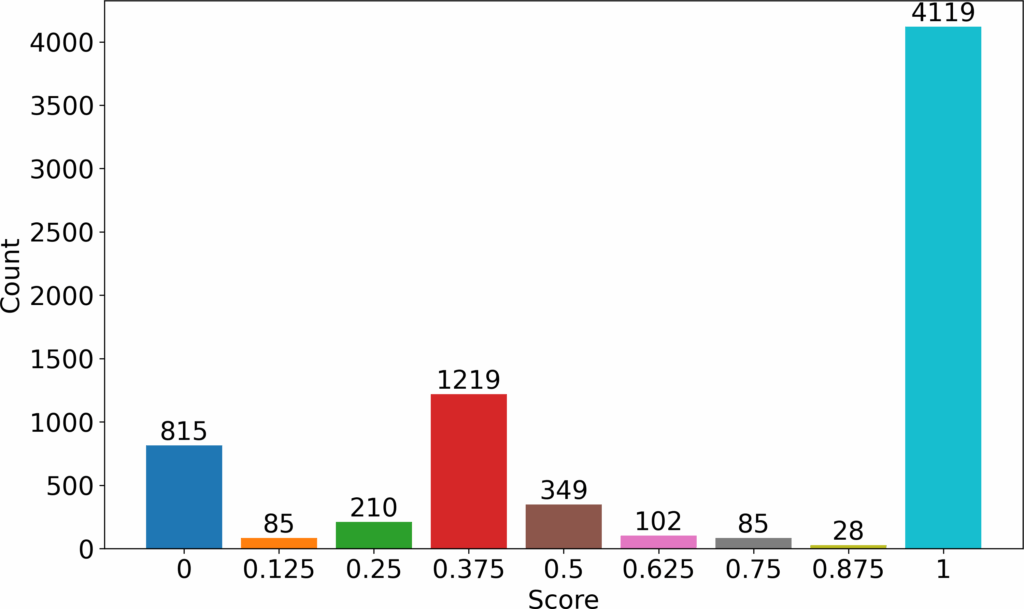
We experimented with the correctness model discussed above for an automated grading system of SQL exercises in a first year’s course at a first year’s BSc course, Information Modelling and Databases at Radboud University. During this study, the course had 309 students. For the year 2023, we used the model to grade 5 quizzes containing more than 25 different questions using the three different matrices. These are shown in a cumulative graph, Figure 1. From the graph, we see that the grading model can differentiate student answers among 9 different groups. We will discuss 3 results from this large sample.

5.1. Introductory stage grading

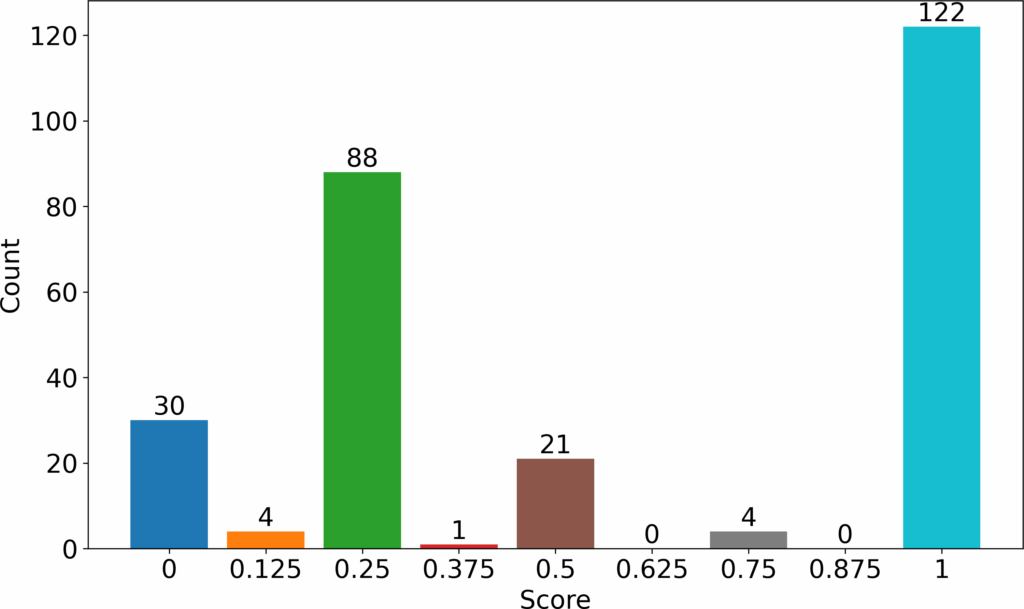
The first question was graded as an introductory quiz. Syn- tax was prioritized more than the other properties. The grades awarded for this question are shown in Figure 2. The x-axis shows the grades given in the range 0 to 1. The y axis show the total number of queries given a certain grade.

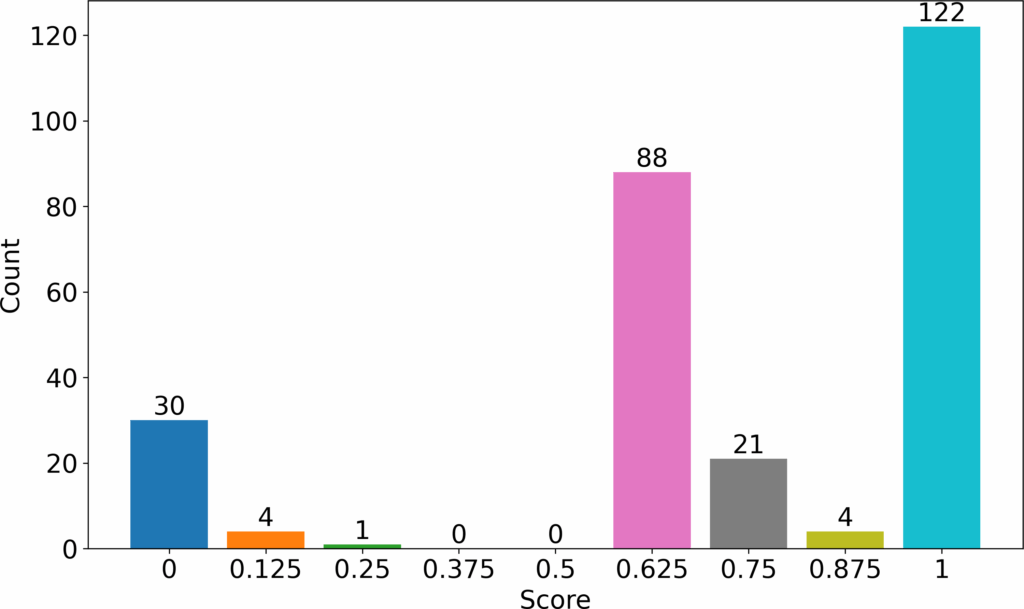
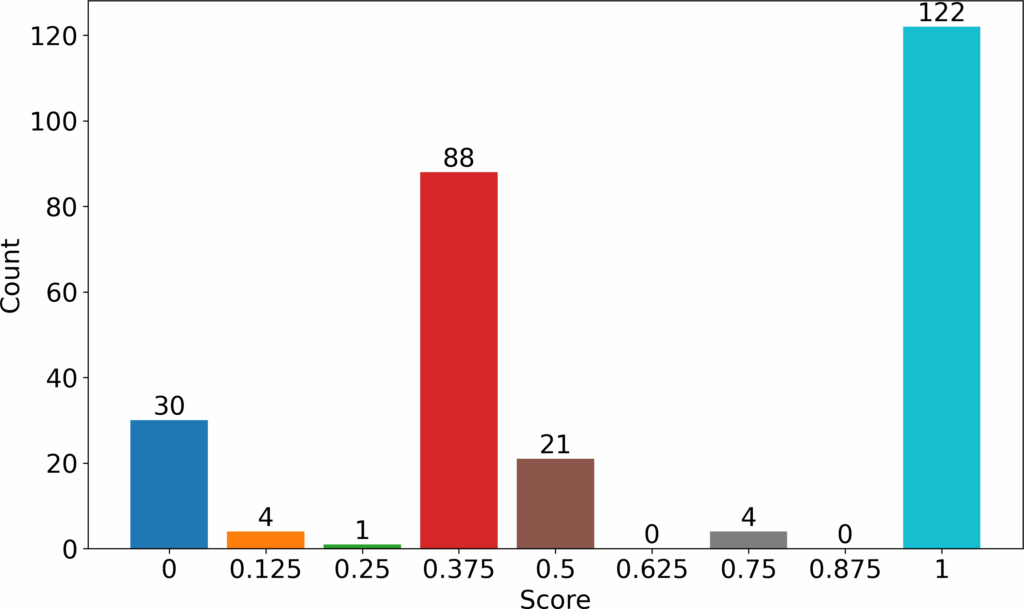
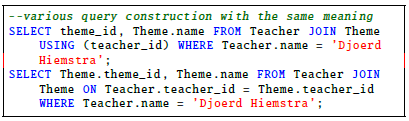
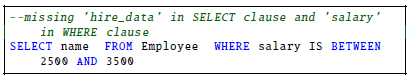
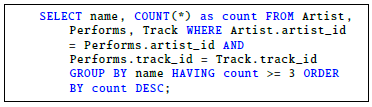
We saw that most students were able to write correct SQL statements (122 students). This group of students could already write syntactically correct SQL that accomplished the given task. The second largest group could form correct syntax SQL queries but could not yet translate these into semantically correct queries (88 students). Taking 0.6 as the passing threshold (parseable queries), 35 students represented by 0, 0.125 and 0.25 grades failed the first question. The other 235 students passed. Grading the same question while prioritizing semantics would have produced the results shown in Figure 3. In this grading, the number of students who passed would have reduced to 126. Lastly, grading the question while prioritizing results would have produced the results shown in Figure 4. In this case, the number of students who passed would have stayed the same as in previous case. However, the grades of those who failed would have reduced even further especially the large group of 88 answers. The reference correct query for this question is shown below.

The student answers for this question fell into the following groups:

(1) 122 answers were fully correct.

(2) 4 answers had minor incorrect semantics (tree edit distance of 1 and text edit distance of less than 3 from a reference query), and correct syntax and results.

(3) 21 answers had minor incorrect results (output of the reference correct query is a subset of the query’s output), incorrect semantics and correct syntax.

(4) 88 answers managed only correct syntax.

(5) 1 answer had minor incorrect syntax (text edit distance of less than 3 from a reference query) and results, and incorrect semantics.

(6) 4 answers had minor incorrect syntax, and fully incorrect results and semantics.

(7) 30 answers had fully incorrect properties.

From the three graphs ( Figure 2, Figure 3, and Figure 4), we see that the grouping stays the same. What changes is the grades awarded to the various groups seen. We also see that the grading progressed from lenient to stringent as we progress from grading using syntax, to semantics and finally results. For this reason, we focus on syntax to carry out introductory stage grading whereby we do not penalize novice students for not meeting higher standard as expected of the more advanced students. We strive to make an impression to the novice students that the new language presented is within their learning capability.

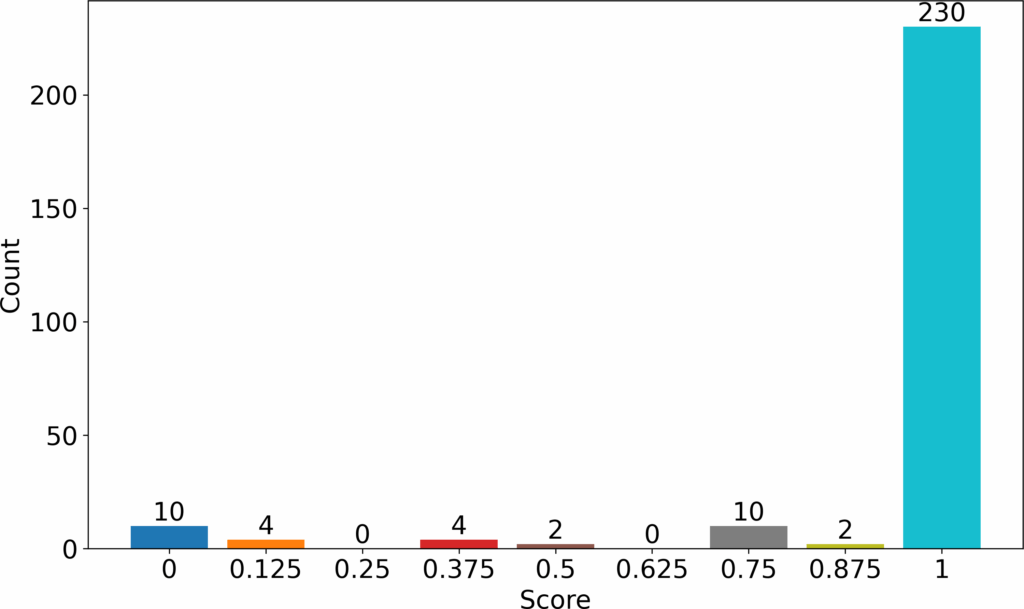
5.2. Intermediate stage grading

As the course progressed the next questions were graded as intermediate quizzes. In this subsection, we give an example of a question which was graded in this intermediate stage whereby, semantics were prioritized more than the other properties. The grades awarded for this question are shown in Figure 5. In the grades evaluated, we saw that almost the whole class (230/262) was able to write semantically fully correct queries. 18 students (0, 0.125 and 0.375 grades) got less than a half point therefore failed this exercise. The reference correct query for this question is shown below.

The student answers for this question fell into the following groups:

(1) 230 answers were fully correct.

(2) 2 answers answers had minor incorrect syntax, and correct semantics and results.

(3) 10 answers had minor incorrect semantics, and correct results and syntax.

(4) 2 answers had minor incorrect results, fully incorrect semantics and correct syntax.

(5) 4 answers had fully incorrect results and semantics, and fully correct syntax.

(6) 4 answers had fully incorrect results and semantics, and minor incorrect syntax.

(7) 10 answers had fully incorrect properties.

5.3. Advanced stage grading

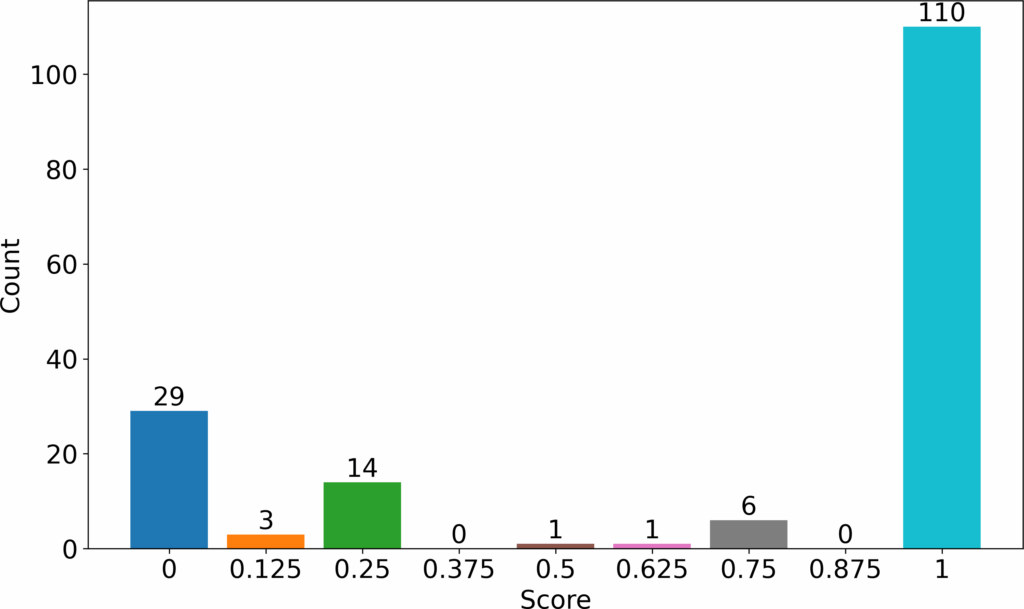
As the course progressed to the final lessons, the questions given were graded as advanced quizzes. In this subsection, we give an example of a question which was graded in this advanced stage whereby, results were prioritized more than the other properties. The grades awarded for this question are shown in Figure 6. In these results, we saw that many students (110/164) managed to write fully correct queries. The second largest group (29/164) students wrote a fully incorrect query even though this groupwas small compared to those who wrote fully correct queries. The rest of the small groups were distributed among various scores. The
reference correct query for this question is shown below.

The student answers for this question fell into the following groups:
(1) 110 answers were fully correct.

(2) 6 answers had fully correct results and syntax but minor incorrect semantics.

(3) 1 answer had fully correct results but minor incorrect syntax and semantics.

This single query was incorrectly graded due to an error in the implementation which we rectified afterwards.

(4) 1 answer had fully correct syntax but minor incorrect results and fully incorrect semantics.

(5) 14 answers had fully correct syntax but fully incorrect results and semantics.

(6) 3 answers had minor incorrect syntax and fully incorrect results and semantics.

(7) 29 answers had fully incorrect semantics, results and syntax.

5.4. Comparison with manual grading

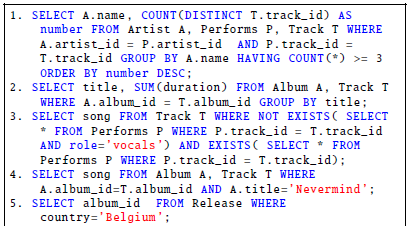
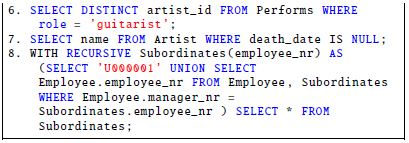
To validate the capabilities of our implementation, we carried a comparison between the grades awarded for the end exam by the instructor, and those calculated by our automated grading system. The instructor evaluated the students not as novices but as learners already familiarized with SQL concepts and knowledge. Our grading system evaluated the queries as advanced quizzes to match the instructor’s grading strategy using the model shown in Table 3. The correct answers to the questions are shown below.

In the comparison, we checked the difference to the grades given for each question using the equation shown below:

$$\textit{difference} = \textit{our\_grade} – \textit{instructor\_grade}\tag{2}$$

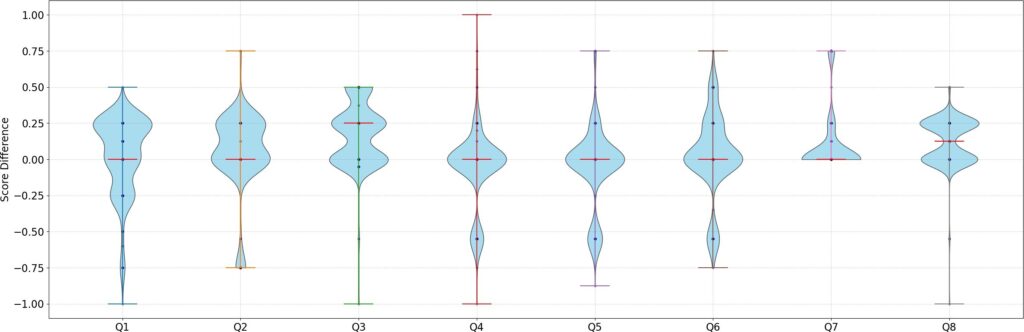
The frequency of differences seen are summarized in Table 4. In the table, score diff. is the difference between the grade given by the automated grading system and by the instruc- tor. Q1 to Q8 are the 8 questions. Each cell in the questions’ columns contain the total number of queries with a given grade difference in that question. The total column show the total number of queries for a given difference in all the questions. These are further illustrated using violin plots in Figure 7. In the figure, Q1 to Q8 are the eight questions. Each question has its own violin plot. The score difference is the difference between the grade given by the automated grading system and by the instructor.

Table 4: The frequencies of differences. Q1 to Q8 are the 8 questions. Diff. is the difference value.

We calculated the mean absolute difference (MAD) and the root mean square error (RMSE) between the two types of grading which was 0.16 and 0.07 respectively using Equa- tion 3 and Equation 4

$$MAD = \frac{1}{n} \sum_{i=1}^{n} |x_i – y_i|\tag{3}$$

$$RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i – y_i)^2}\tag{4}$$

Whereby n is the total number of differences, x is a grade given by our system and y is a grade given by the instructor. This difference between the two systems comes from the following main observations which are summarized below:

1. 1093 queries received the same score in both cases. These were fully correct queries and fully incorrect queries.

2. 550 queries received a 0.25 score higher in our automated grading system. These were incorrect queries that were at least parseable. Our grading acknowledged that even though these students did not learn correct SQL semantics, they were able to form correct SQL syntax.

3. 121 queries received a 0.55 score higher from the instructor. These were correct queries containing unexpected special characters, for example:

The instructor deducted a 0.2 from the score while our system struggled to correctly evaluate such queries.

4. 81 queries received a 0.5 score higher in our system. These were queries which were semantically incorrect with correct results as a subset of the queries’ results.

5. 48 queries received a 0.25 score higher from the instructor. Most of these differences were from the first question. The instructor gave a 0.5 to those answers that demonstrated that the student clearly understood the semantics of the question but could not fully translate it to the complete query. For example:

Our system failed to evaluate this and gave a 0.25.

6. 34 answers received a 0.75 score higher in our system. These were queries whose semantics were minor incorrect. For example, 17 queries contained:

This query used a comparing operator for NULL instead of using IS NULL. The instructor observed that they were strict in this case.

7. 23 queries received a 0.75 higher score from the instructor. These were queries which were graded as fully correct by the instructor . Our system evaluated them as incorrect. For example:

The query did not group by ’title’ therefore it was considered as incorrect by our system.

As we seen in Figure 7, most differences between instructor’s grading are within 0.25 score (horizontal bulges). We have highlighted the major differences seen above. In some cases, the instructor was strict as seen from the 34 queries in item 6 and item 4. In other cases, the instructor was lenient in grading as seen in queries in item 5 and item 7. In comparison, our grading was consistent across different queries. This consistency aided our system to allocate fair grades with some exceptions. These are cases whereby the system failed to capture special unexpected non-SQL characters as seen in item 3.

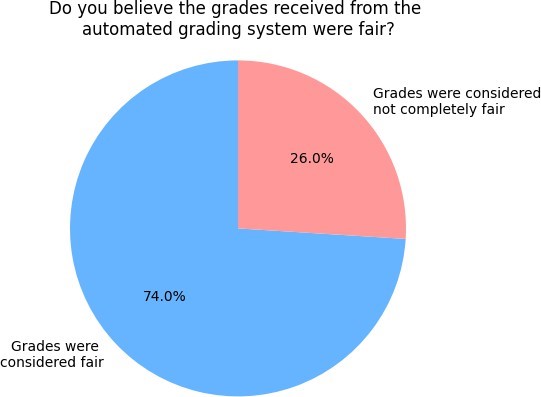
At the end of the experiment, we administered a questionnaire to the students. We let them know that the questionnaire was useful in that, we would use their answers to improve the grading system. The students based their answers on the grades received since we carried out the grading using the system and sent them their results. This included some feedback text. For example, SYNTAX: Correct! Well done. RESULTS: The output of the query is not correct. SEMANTICS: The query does not have correct semantics. This quiz was graded as an advanced quiz. We placed more weight on results, then semantics and finally syntax. A group of 46 students present at the time participated in the questionnaire, in which we enquired about their opinion on the automatically given grades. For example, we asked them if they considered the grades received as fair or not. This was to verify that indeed the students found the grades given acceptable. The results are shown in Figure 8. We saw that 74% said the grades received were fair while the rest 26% considered the grades not completely fair. Some students observed our system being not completely fair in those cases our implementation failed to catch minor incorrect syntax, for example for those unparseable queries containing random characters that proved difficult to automatically identify and repair. We plan to work on this in our next implementation.

5.5. Configuration variables

In our method, there are 6 configuration variables that affect the grading (number of syntax outcomes, number of semantics outcomes, number of results outcomes, property weight, text edit distance threshold and tree edit distance threshold). Changing these variables alters the grading in different ways. The first 3 variables affect the number of outcomes for the different properties. The fourth variable affects which property is focused more when grading. The fifth variable is the threshold value for syntax analysis edit distance calculation. Lastly, the sixth variable is the thresh- old for the semantics tree edit distance calculation. All these variables can be adjusted to change how grading is done. The threshold parameter for edit distances for syntax and semantics in this experiment were set to 2 and 1 respectively. In our next implementation we plan to study in detail how changing these variables will affect the grades awarded.

6. Discussion

During the introductory period of our course, one of the main goals was for the students to learn the correct SQL syntax and grammar. It was crucial for the students to be able to form SQL queries that can be parsed. In our first quiz, we tested whether the students had indeed understood how syntactically correct SQL queries are written. We graded the quiz focusing mostly on syntax with semantics and results being secondary. This grading model is shown in Table 1. Our results from Figure 2 showed that this goal was accomplished as most students (235/270) were able to form syntactically correct SQL queries. These students scored more than 0.6. Furthermore, a large number (122/270) were able to write semantically correct queries. This meant that the teaching could proceed onto the next stage, which is using SQL to accomplish the given tasks.

In the next stage of learning, the students could already write syntactically correct SQL queries. This was the intermediary stage, whereby the goal was using SQL to carry out the given tasks. The quizzes in this stage were graded focusing mostly on semantics while syntax and results were secondary. This grading model is shown in Table 2. In one of the questions, shown in Figure 5, most of the students (230/262) could translate SQL into statements that could accomplish the given task.

We graded the last quizzes for the course as advanced quizzes. At this stage the students could write the correct SQL grammar and write semantically correct queries. Therefore, when grading, we focused mostly on results while semantics and syntax were secondary. Many students were able to write queries with the correct results (110/164 students). The grading model used is shown in Table 3.

7. Conclusion

In this paper, we have demonstrated a model for generating discrete levels that enable effective partial grading of SQL queries. We call these discrete levels, software correct- ness levels that translate into partial grades. We have also demonstrated how we can be able to offer personalized and differentiated type of grading depending on the knowledge level of the students. This is in contrast to the previous research that utilize inflexible methods. we divided the learning process into 3 stages and applied specific types of grading to each stage. These stages were introductory, intermediate, and advanced. At each stage of our course, we were able to focus the grading on a specific goal which depended on the skills of the students. This is dynamic grading. Dynamic grading was enabled by weighing some properties like syntax more than others at specific points of the teaching process. Partial grading was enabled by indi- vidually evaluating different properties in such a way that their outcomes are categorized, for example in categories like correct, minor incorrect and fully incorrect. In our cur- rent implementation, we worked with the properties syntax, semantics, and results, and we generated corresponding correctness levels for those properties. In partial grading we utilized software correctness levels while in dynamic grading, we considered students’ skills level. This helped us to effectively provide partial grades that were dependent upon the skill or knowledge level of students at different stages of their learning process.

We observed that our grading model had some differences in the grades calculated from those awarded by the instructor. We evaluated these differences from SQL questions from an exam and observed a mean average difference of 0.16. We also administered a questionnaire to 46 students whereby 74% observed that our implementation of the model discussed was able to calculate grades they considered fair. Nevertheless, there were limitations which we plan to address in both the grading model and its implementation. For the implementation, we plan on improving on: handling unexpected special non-SQL characters, checking query results against more than 1 data schema, extending the supported queries to include, Create, Delete, Insert and Update and a clear separation between syntax and semantics analysis. The later limitation resulted in missing groups for example, [syntax: minor incorrect, result: correct]. For the model, we plan on adding another property or outcome for more sensitivity and to evaluate the optimum configuration for the minimum difference between the grades awarded by the system and the instructor. More thorough work is needed to present the full merits of the discussed model.

1. T. Seifert, “Understanding student motivation”, Educational Research, vol. 46, no. 2, pp. 137–149, 2004, doi:10.1080/0013188042000222421.
2. B. Chandra, A. Banerjee, U. Hazra, M. Joseph, S. Sudarshan, “Au- tomated grading of SQL queries”, “2019 IEEE 35th International Conference on Data Engineering (ICDE)”, pp. 1630–1633, 2019, doi:10.1109/ICDE.2019.00159.
3. G. Dambić, M. Fabijanić, A. L. Ćošković, “Automatic, configurable and partial assessment of student SQL queries with joins and group- ings”, “2021 44th International Convention on Information, Com- munication and Electronic Technology (MIPRO)”, pp. 837–842, 2021, doi:10.23919/MIPRO52101.2021.9596680.
4. M. Fabijanić, G. Dambić, J. Sasunić, “Automatic, configurable, and partial assessment of student SQL queries with subqueries”, “2022 45th Jubilee International Convention on Information, Communi- cation and Electronic Technology (MIPRO)”, pp. 542–547, 2022, doi:10.23919/MIPRO55190.2022.9803559.
5. J. Kjerstad, “Automatic evaluation and grading of SQL queries using relational algebra trees”, Master’s thesis, Norwegian University of Science and Technology, 2020.
6. T. J. McGill, S. E. Volet, “A conceptual framework for analyz- ing students’ knowledge of programming”, Journal of Research on Computing in Education, vol. 29, no. 3, pp. 276–297, 1997, doi:10.1080/08886504.1997.10782199.
7. B. Shneiderman, R. Mayer, “Syntactic/semantic interactions in pro- grammer behavior: A model and experimental results”, Interna- tional Journal of Parallel Programming, vol. 8, pp. 219–238, 1979, doi:10.1007/BF00977789.
8. B. Shneiderman, “Teaching programming: A spiral approach to syn- tax and semantics”, Computers & Education, vol. 1, no. 4, pp. 193–197, 1977.
9. A. Stefik, S. Siebert, “An empirical investigation into programming language syntax”, ACM Transactions on Computing Education (TOCE), vol. 13, no. 4, pp. 1–40, 2013.
10. K. Renaud, J. van Biljon, “Teaching sql — which pedagogical horse for this course?”, H. Williams, L. MacKinnon, eds., “Key Technologies for Data Management”, pp. 244–256, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004.
11. P. Garner, J. A. Mariani, “Learning sql in steps”, Journal on Systemics, Cybernetics and Informatics, vol. 13, pp. 19–24, 2015.
12. H. Al Shauily, K. Renaud, “A framework for sql learning: linking learning taxonomy, cognitive model and cross cutting factors”, Inter- national Journal of Computer and Systems Engineering, vol. 10, no. 9, pp. 3105–3111, 2016.
13. A. Bhangdiya, B. Chandra, B. Kar, B. Radhakrishnan, K. V. M. Reddy, S. Shah, S. Sudarshan, “The XDa-TA system for automated grading of SQL query assignments”, 2015 IEEE 31st International Conference on Data Engineering, pp. 1468–1471, 2015.
14. S. Dekeyser, M. de Raadt, T. Y. Lee, “Computer assisted assessment of SQL query skills”, “Proceedings of the Eighteenth Conference on Australasian Database – Volume 63”, ADC ’07, p. 53–62, Australian Computer Society, Inc., AUS, 2007.
15. M. Gilsing, J. Pelay, F. Hermans, “Design, implementa- tion and evaluation of the hedy programming language”, Journal of Computer Languages, vol. 73, p. 101158, 2022, doi:https://doi.org/10.1016/j.cola.2022.101158.
16. J. C. Prior, R. Lister, “The backwash effect on SQL skills grading”, “Proceedings of the 9th Annual SIGCSE Conference on Innovation and Technology in Computer Science Education”, ITiCSE ’04, p. 32–36, Association for Computing Machinery, New York, NY, USA, 2004, doi:10.1145/1007996.1008008.
17. M. Kramer, M. Barkmin, D. Tobinski, T. Brinda, “Understanding the differences between novice and expert programmers in memoriz- ing source code”, A. Tatnall, M. Webb, eds., “Tomorrow’s Learning: Involving Everyone. Learning with and about Technologies and Com- puting”, pp. 630–639, Springer International Publishing, Cham, 2017.
18. M. Weiser, J. Shertz, “Programming problem representation in novice and expert programmers”, International Journal of Man-Machine Studies, vol. 19, no. 4, pp. 391–398, 1983, doi:https://doi.org/10.1016/S0020- 7373(83)80061-3.
19. C. M. Zeitz, “Expert-novice differences in memory, abstraction, and reasoning in the domain of literature”, Cognition and Instruction, vol. 12, no. 4, pp. 277–312, 1994.
20. M. T. Chi, P. J. Feltovich, R. Glaser, “Categorization and representation of physics problems by experts and novices”, Cognitive Science, vol. 5, no. 2, pp. 121–152, 1981.
21. L. E. Winslow, “Programming pedagogy—a psychological overview”, SIGCSE Bulletin, vol. 28, no. 3, p. 17–22, 1996, doi:10.1145/234867.234872.
22. A. Robins, J. Rountree, N. Rountree, “Learning and teaching program- ming: A review and discussion”, Computer science education, vol. 13, no. 2, pp. 137–172, 2003.
23. B. Xie, D. Loksa, G. L. Nelson, M. J. Davidson, D. Dong, H. Kwik, A. H. Tan, L. Hwa, M. Li, A. J. Ko, “A theory of instruction for introductory programming skills”, Computer Science Education, vol. 29, no. 2-3, pp. 205–253, 2019, doi:10.1080/08993408.2019.1565235.
24. C. Wilcox, “Testing strategies for the automated grading of stu- dent programs”, “Proceedings of the 47th ACM Technical Sympo- sium on Computing Science Education”, SIGCSE ’16, p. 437–442, Association for Computing Machinery, New York, NY, USA, 2016, doi:10.1145/2839509.2844616.
25. C. Benac Earle, L.-r. Fredlund, J. Hughes, “Automatic grading of pro- gramming exercises using property-based testing”, “Proceedings of the 2016 ACM Conference on Innovation and Technology in Computer Science Education”, ITiCSE ’16, p. 47–52, Association for Computing Machinery, New York, NY, USA, 2016, doi:10.1145/2899415.2899443.
26. P. Runeson, “A survey of unit testing practices”, IEEE Software, vol. 23, 2006, doi:10.1109/MS.2006.91.
27. B. Wanjiru, P. v. Bommel, D. Hiemstra, “Towards a generic model for classifying software into correctness levels and its application to SQL”, “2023 IEEE/ACM 5th International Workshop on Software Engineering Education for the Next Generation (SEENG)”, pp. 37–40, 2023, doi:10.1109/SEENG59157.2023.00012.
28. B. Wanjiru, P. v. Bommel, D. Hiemstra, “Sensitivity of automated SQL grading in computer science courses”, “Proceedings of the Third International Conference on Innovations in Computing Research (ICR’24)”, 2024.
29. C. Kleiner, C. Tebbe, F. Heine, “Automated grading and tutoring of sql statements to improve student learning”, “Proceedings of the 13th Koli Calling International Conference on Computing Education Research”, Koli Calling ’13, p. 161–168, Association for Computing Machinery, New York, NY, USA, 2013, doi:10.1145/2526968.2526986.
30. B. Chandra, B. Chawda, B. Kar, K. V. M. Reddy, S. Shah, S. Sudarshan, “Data generation for testing and grading sql queries”, The VLDB Journal, vol. 24, no. 6, p. 731–755, 2015, doi:10.1007/s00778-015-0395-0.
31. S. Chaudhuri, “An overview of query optimization in relational systems”, “Proceedings of the Seventeenth ACM SIGACT-SIGMOD- SIGART Symposium on Principles of Database Systems”, PODS ’98, p. 34–43, Association for Computing Machinery, New York, NY, USA, 1998, doi:10.1145/275487.275492.
32. K. Ala-Mutka, T. Uimonen, H.-M. Järvinen, “Supporting students in C++ programming courses with automatic program style assessment”, JITE, vol. 3, pp. 245–262, 2004, doi:10.28945/300.
33. F. G. Wilkie, B. Hylands, “Measuring complexity in C++ application software”, Software: Practice and Experience, vol. 28, 1998.
34. N. R. Tallent, J. M. Mellor-Crummey, “Effective performance mea- surement and analysis of multithreaded applications”, PPoPP ’09, p. 229–240, Association for Computing Machinery, New York, NY, USA, 2009, doi:10.1145/1504176.1504210.
35. M. Raasveldt, H. Mühleisen, “Duckdb: an embeddable analyt- ical database”, “Proceedings of the 2019 International Confer- ence on Management of Data”, SIGMOD ’19, p. 1981–1984, As- sociation for Computing Machinery, New York, NY, USA, 2019, doi:10.1145/3299869.3320212.
36. T. pganalyze Developer Team, “libpg_query”, 2023, version 15-4.2.1.
37. L. Yujian, L. Bo, “A normalized levenshtein distance metric”, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 29, no. 6, pp. 1091–1095, 2007, doi:10.1109/TPAMI.2007.1078.
38. K. Zhang, D. Shasha, “Simple fast algorithms for the editing distance between trees and related problems”, SIAM J. Comput., vol. 18, pp. 1245–1262, 1989, doi:10.1137/0218082.

Citations by Dimensions

Citations by PlumX

Crossref Citations

This paper is currently not cited.

No. of Downloads per Month

No. of Downloads per Country