In this study, exact trigonometric displacement function was used to solve the buckling problem of a three-dimensional (3-D) rectangular plate that is clamped at the first-three edges and the other remaining edge simply supported (CCCS) under uniaxial compressive load. Employing 3-D constitutive relations which consist of entire components, the functional for total potential energy was obtained. After that, the rotation and deflection at x-axis and y-axis were formulated from the established compatibility equations to get an exact trigonometric deflection function. The characteristics equation was obtained by differentiating energy equation with respect to deflect to obtain the relations between deflection and rotation. The equation of the total potential energy is minimized with respect to the deflection coefficient after incorporating the deflection and rotation function, the critical buckling load formula was established. The solution for the buckling problem gotten shown that the structure of the plate is safe when the plate thickness is increased as the outcome of the study showed that the critical buckling load increased as the span- thickness ratio increased. The overall difference in form of percent between the present work and previous studies recorded is 5.4%. This shows that at about 95% certainty, the present work is perfect. The comparison of this study with the results of previous similar studies revealed the uniformity 3-D plate theory and the variations of CPT and RPT theories in the exact buckling analysis of a rectangular plate. However, this approach which includes all the six stress elements of the plate material in the analysis produced an exact deflection function unlike the previous studies which used assumed functions. Furthermore, the theoretical analysis of this study demonstrates a novel approach to solve the buckling problem rectangular plate which is capable of analyzing rectangular plates of any thickness configuration.

1. Introduction

Plates are three dimensional elements that comprises of two large plane perpendicular surfaces detached by a thickness [1, 2] and its application is widely seen in several engineering fields such as aeronautics, astronautic engineering, structural industries and marine structures. In recent years, the use of plates has greatly increased as a result of some benefits such as its versatility, affordability lightweight and its ability to resist heavy loads [3].

It is essential to examine the geometry of the plates and their supports, the behavior of the material used, the type of loads and their method of application; due to its complexity [4]. Plates can be rectangular, square or circular in shape. Based on the materials of construction, plates can be anisotropic, isotropic and orthotropic. The plates also have free edge, simply supported and fixed supported edge conditions [5]. Plates can also be classified as thin, thick and moderately thick plates based on their thickness [6, 7]. Based on span-to-depth ratio, [7] considered 𝑎/𝑡 ≤ 10 as thick plate, 15 ≤ 𝑎/𝑡 ≤ 40 as moderately thick plate and 𝑎/𝑡 ≥ 45 as thin plate. The importance of thick plate and its wide application in different aspects of engineering has necessitated more researches so as to maximize its application potential.

The bending, vibration and the buckling of plates are research areas for analyzing thick plates [8]. The phenomenon where a critical load value without further load application makes a material under the influence of in-plane loads to move from a stable to unstable equilibrium state is called buckling [9]. Buckling of plates can be classified as elastic and inelastic. For elastic buckling analysis, when the plate is stressed beyond the elastic limit before the beginning of buckling, it is said to be an inelastic or plastic buckling problem [10]. When the in-plane compressive load is increased beyond their critical values, the outcome is totally plate failure. Many scholars have employed different methods to solve the elastic buckling problems of thick plates. Generally, these methods include the equilibrium (Euler) methods, numerical methods, and energy methods [7].

Equilibrium methods such as the Fourier series method, the methods of integral transformation, Navier’s double trigonometric series method, and the separation of variables method; Subject to the restraints of the plate edges and the loading boundary conditions, yields closed form solutions to the governing partial differential equations of equilibrium of the elastic buckling problem of plates within the domain of the plate [11]. However, the limitation of this method is that their application to plates with fixed edges, free edges and mixed support condition results in analytical difficulties. Numerical methods such as finite difference methods, finite strip methods, the finite element methods, and boundary element methods; yield approximate numerical solutions of the plate problem. Energy methods such as Rayleigh-Ritz method, Ritz variational method, and Kantorovich variation method, are methods of investigating the elastic buckling behavior of plates based on the application of the minimum principle to the total potential energy of the plate buckling problem. To obtain the characteristic buckling equation whose roots yields the buckling loads, energy methods minimize the total energy function of the plate’s elastic buckling problem as regards to the parameters of the shape function.

A series of theories have been developed and employed to investigate the stability of plates. Such theories include the classical plate theory (CPT) and the refined plate theory (RPT). The CPT is a plate theory that ignores shear deformation that is lying across it, which is mostly used for analyzing thin plates [12]. The CPT overestimates buckling loads, natural frequencies and underestimates deflections for moderately thick or thick plate. It is inadequate for thick plate’s analysis as a result of neglected transverse shear strains.

The refined plate theory (RPT) was formulated to overcome the limitations of the CPT. The RPT proposed by authors in [13] and [14] addressed vertical shear deformation effect in plate analysis. The RPT include; First order shear deformation theory (FSDT), Second order shear deformation theory (SSDT). To produce accurate results, the FSDT and SSDT require a shear correction factor. It is difficult to obtain exact values because the shear correction factor depends on parameters such as support case, loading type and geometry. The High-order shear deformation theory (HSDT) was developed in order to consider the shear deformation effect without the factor of shear correction in plate analysis and to achieve a real difference between transverse shear stress at the plate surfaces [15]. The negligence of normal stress and strain along the thickness axis of the plate, makes the refined plate theory inconsistent, hence it can be addressed as a 2-D theory or an incomplete 3-D theory [16].

Employing a modified Stowell’s technique, the authors in [16] investigated the buckling of an isotropic rectangular plate that is uniaxially loaded with a free edge that is not loaded. The authors considered plates with edge conditions of SCFC, CSFS, SSFS, CCFC, CSFC and SCFS. Applying polynomial functions from Taylor-Maclaurin series for each plate, the shape function was first determined. For different values of aspect ratio and moduli ratio, the authors presented the coefficients of buckling of each plate. Although their findings agreed reasonably with previous works, their study did not address a thick plate nor was a CCCS edge condition considered. The authors also did not employ the trigonometric functions.

To investigate the buckling behavior of a rectangular thick plate subjected to uniaxial in-plane compressive loading, the authors in [17] applied polynomial displacement functions. The direct governing equation which was obtained from orthogonal polynomial displacement functions, was solved to obtain the equation used to obtain the parameters for the determining buckling load. Although their results so similar when compared with previous studies as they did not involve CCCS edge condition and did not take trigonometric function into account.

The authors in [18] employed a split-deflection method and applied to the buckling analysis of thin rectangular plates under vibration. They also applied trigonometric to obtain the governing equation of the plate’s equilibrium forces which was solved to get deflection function for  CCCS rectangular plate analysis; their study did not address a thick plate as their assumption is limited to CPT which will not yield a good result when the plate is relatively thick.

The shape function derived from polynomial series was applied in the work of authors in [19] to determine the buckling behavior of the isotropic rectangular plate using the Ritz method. The authors substituted the shape function into the potential energy function, which was later minimized and the critical buckling load was obtained. The authors did not take into account a three dimensional CCCS thick plate. There was also no consideration for trigonometric function to ensure the exact solution rather than other shape function whose solution cannot be reliable for analysis of thick and moderately thick plate [20].

The third-order energy functional was used by authors in [21] to investigate the buckling of CCSS and CCCS isotropic rectangular plates. At every point in the plate within the plate domain and adding the product of the stress and strain, the authors formulated third order strain energy. To get the total energy functions of third order, strain energy was also summed with the external load. The method of direct variation was adopted to actualize this. Although the results of their study showed some degree of accuracy when compared to previous works, they did not consider the application of trigonometric displacement function.

Variation energy method was used by authors in [22] to analyze the buckling of a 3-D CCCC thick plate applying both polynomial and trigonometric function. Although the three-dimensional plate theory and the uniaxial compressive load were applied, the authors failed to consider a thick plate with the CCCS boundary condition.  The buckling of isotropic stiffened CCCC plate was investigated by the authors in [23]. The authors employed the use of the work principle approach and varied the aspect ratios, the properties of stiffness and the number of stiffeners, to analyze the critical buckling of the plates. The shape function was theoretically derived using Taylor Maclaurin’s displacement function. The authors in [23] did not apply trigonometric displacement function and 3-D plate theory. The CCCS plate was not addressed in both studies. Since a thick plate is a typical three-dimensional structural element and not much work has been done applying 3-D plate theory, this present study is necessary.

Considering the approach of exact displacement function, the authors in [24, 25 and 26] obtained an analytic solution for the elastic buckling analysis of plates. The authors derived the displacement function from the compatibility equation to get a close form solution for 3-D stability analysis of thick plate under uniformly distributed load. The authors in [25] did not apply trigonometric function which predict the exact buckling load and both authors [24, 25 and 26] did not address isotropic thick plates with three clamped edges and one simply supported edge (CCCS).

The physical interpretation of CCCS plate is that, the three clamped edges are supported by a column and the other supported a beam, depicting the relevance of the present study. This is because the boundary condition depends on the type of beam/column support in the plate, thus when CCCS initial condition occurs in the a plate material, analyzing it as any other type of plate as mentioned in the literature will not account for stresses induced. This is because, stresses are induced due to the applied load (in-plane load) in this case, and hence, non-negligible error results.

This work filled the gap as they applied the variation energy method with a trigonometric displacement function to get an exact three-dimensional stability rectangular plate under uniaxial compressive load. The focus of this study is to determine the calculating formula for the critical buckling load of thick plate that was clamped at the three edges and other edge simply supported (CCCS). Furthermore, the aspect ratio effect of the critical buckling load of the plate was evaluated to show its capacity to analyze different categories of plate, ranging from thin, thick and moderately thick plate.

2. Methodology and Theoretical Analysis

The theoretical analysis of this study lies in the buckling behavior of a three-dimensional rectangular plate’s material based on exact trigonometric plate theory. This study demonstrates a novel approach to solve the buckling problem of a three-dimensional CCCS rectangular plate subjected to compressive load. In this work, and displacement in x, y and z axis; u, v and w respectively are applied and presented in Equation (1), (2) and (3) (see [22]):

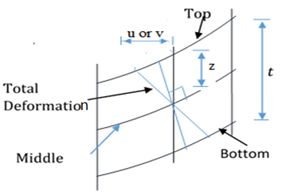
It can be seen in figure 1, that the six strains and stress elements required for the analysis were determined in line with the work of authors in [22].

2.1. Formulation of Total Potential Energy

The energy  equation were obtained in line with the authors in [23] and presented as:

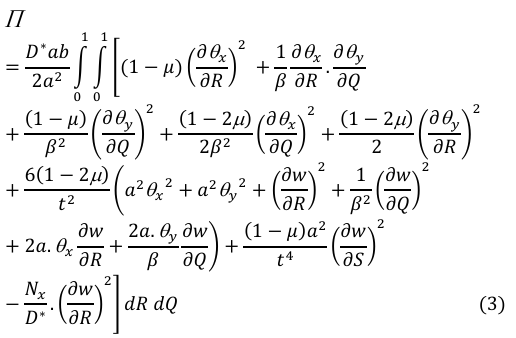
Where;  is the uniform applied uniaxial compression load of the plate.

2.2. Compatibility Equations

According to the work of authors in [24], the compatibility equation was obtained by differentiation of total potential energy with respect to  to establish the relationship between the rotation and deflection:

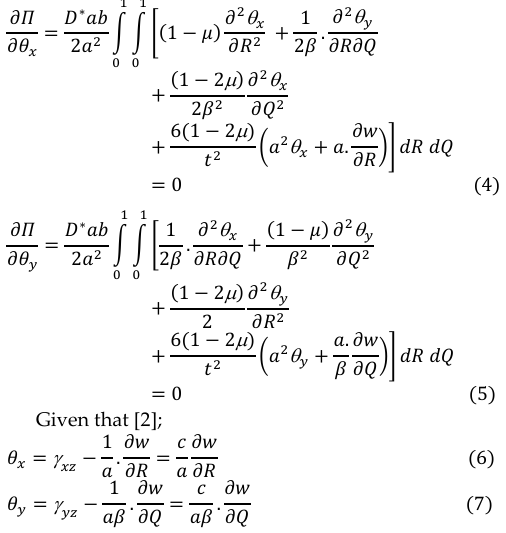
Hence, for zero integrands, the true solution was gotten by simplifying and factorizing the outcome of the compatibility equation to give the algebraic solution in Equation (8) which is the relation of known and unknown variable to get the constant quantity c.

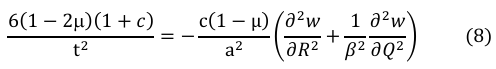
2.3. Governing Equations

The governing differential equation was obtained after the total potential energy was differentiated with respect to deflection (w) and its solution gives the exact deflection function:

The solution of Equation (11) to get an exact deflection
and slope of the plate.

The constants; , thus, putting Equations (13), (14) and (15) into (3), simplifying and gives:

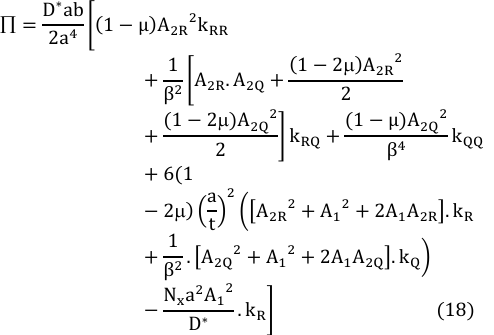
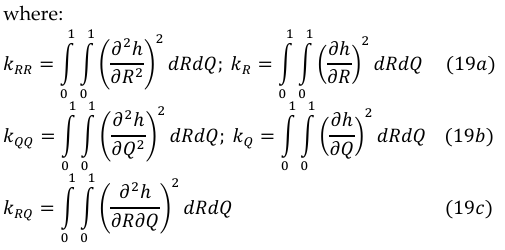
Minimizing Equation (18) with respect to A_2R gives:

Solving Equations (22) and (23) simultaneously gives:

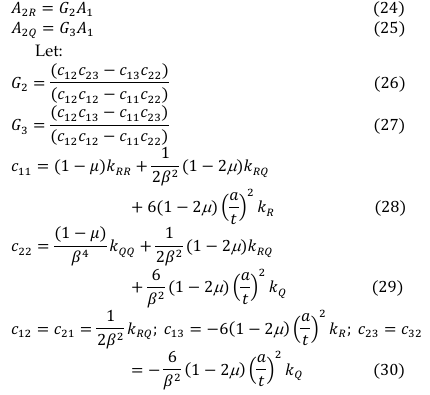
Minimizing Equation (18) with respect to A₁ and simplifying the outcome gives:

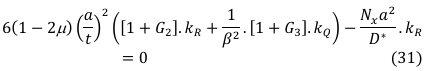
Rearranging Equation (31) and simplify to give:

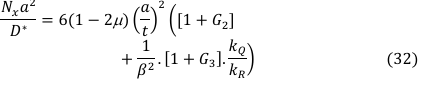
2.4. Formulation of Total Potential Energy

A numerical analysis is performed on the rectangular thick plate that was clamped in the first three edges and remaining edge simply supported under uniaxial compressive load as presented in Figure 2.

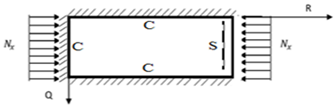
The plate at figure 2 has the following initial conditions:

Putting Equation (33) to (36) into the derived function of deflection gives:

The value of  that satisfies Equation (37) is:

Substituting Equation (38) into the derivatives of w and satisfying the boundary conditions of Equation (33) to (36) gives the following constants:

Substituting the constants of Equation (38) and (39) into Equation (10) and simplifying the outcome gives:

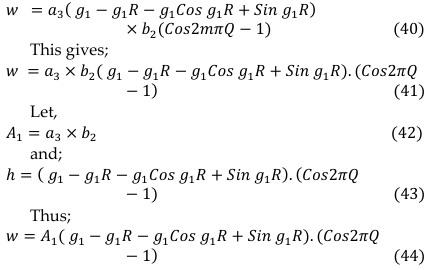
Where;

w and h are deflection and shape function of the plate respectively.

Using the particular trigonometric displacement function presented in Equation (44), the numerical of solution of the stiffness coefficients for deflection of rectangular thick plate analysis subjected to the CCCS boundary condition was obtained and presented.

Let; trigonometric stiffness coefficient values of CCCS plate Where; the Poisson’s ratio of the plate be 0.3.

3. Results and Discussions

The numerical result of the analysis was obtained by employing trigonometric function at a different aspect ratio to get the result of non-dimensional critical buckling load on the three-dimensional CCCS rectangular thick plate presented in Figure 3 through 12. It is observed that the value of the critical buckling load N_x decreases as the value of the aspect ratio (1.0, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8 and 2.0) increases at varying stiffness as shown in Figure 3 through 12. This indicates that the chance of failure in a plate structure increases with an increase in plate width. This value begins to vary as the aspect ratio increases. This is quite expected because the increase in the plate’s aspect ratio decreases the capacity of the plate to resist buckling.

The span to thickness ratio of the plate varies between 4, 7, 10, 15, 20, 30, 40, 50, 60, 70, 80, 90, 100, 1000 and 1500 at the varying breadth of the plate. More so, it is seen in the figures that the results the values of critical buckling load increase as the span- thickness ratio increases. This means that the failure in a plate structure is bound to occur as the in-plane load on the plate increases and gets to the critical buckling. The present theory predicts the buckling load of 64.3, 91.7, 102.5, 109.4, 112.1, 114.1, and 114.8 for a square plate in the span to thickness ratio of 5, 7, 15, 20, 30, and 40. Meanwhile, the value of the buckling load predicted for the same plate beyond the span to thickness ratio of 40 gives a constant value of about 115.4 when corrected to two decimal places. This shows that the result of the critical buckling load of thin and moderately thick plate using the 3-D theory is the same for the stability analysis of rectangular plate under the CCCS boundary condition. But looking at a graphical representation of these results in Figures 3 to 12 shows that at span-thickness ratio of 20 and above the graph appears straight along the horizontal axis. This confirms the study of the authors in [8] which showed that thin and moderately thick plates with the span to thickness ratio are from 20 and above.

In the validation of the result of the present study, a comparative analysis is performed to show the degree of divergence between the result of the present study with those of classical plate theory (CPT) and refined plate theory (RPT) as presented in Table 1&2 and Figure 13. The average percentage difference between the present study and those of authors in [18], [20], [21] and [27] is about 6.33%, 6.37%, 6.47 and 2.59% respectively. Moreover, the result of the result of percentage difference being lower is quite expected because 3-D theory predict more close-form answer to the problem and prudent to use compared to the CPT and RPT.

The overall difference in percentage between the present study and those of 3-D elasticity theory in [27] is about 2.59%, while the average total percentage difference between the values from the present study and those of the 2-D RPT and CPT are 6.35 and 6.47 respectively. Here from, the overall difference in terms of percentage between the present study and those of the 3-D elasticity theory in [27] being lower than 2.6% show high level of insignificance in comparison, therefore debits that present theory gives an exact solution and can be reliable in the 3-D stability analysis of all types of a rectangular plate under such support configuration. From Figures 6, 7 and Table 4, the present study showed good agreement with previous studies but varied widely when considered as a thick plate at span to thickness ratios of 4 and 7. Meanwhile, the average difference in terms of a percentage between the present work and those of CPT in [18] and [20] and 2-D RPT in [21] is higher than 6.4%. It is noticed from the analysis that the present theory converges faster with exact elasticity theory than the CPT and RPT, which proves exactness and dependable nature of the derived relations. Thus, it was discovered that the present study become closer to those obtained using the CPT in [24] and [25] as the span-thickness ratio increases, and closest to those using RPT in [20] for a square plate at span to thickness ratio of 7. It should be noted that the present result when compared with exact elasticity theorem according to the authors in [27] gave a small percentage difference of 2.5%; the value which appears to be almost the same with exact elasticity theorem proves the exactness of the present theory. The result of present work being slightly higher than those of authors in [26] as seen in the Figure 12 does not invalidate the result as it’s quite expected because the present theory which applied trigonometric theory predict more exact answer to the problems and prudent to use compared to other shape functions in the exact stability analysis of the plate. Meanwhile, the result of the present study is obviously higher than those of authors in [18], [20] and [21] because the authors in [18], [20] and [21] did not consider a typical 3-D analogy rather 2-D which was gotten by making suitable assumption to the kinematics of the relation or state of stress through the thickness axis of the plate which make their result inexact.

The result of comparative study confirmed that the 2-D RPT is only an approximate relation while the 3-D trigonometric function established in this study gives an exact solution for stability analysis of plates under the same boundary condition compared to polynomial [27, 28]. However, the overall difference in terms of percent between the present work and past works in comparison is about 5%. This means that at about 95% certainty, the values from the present study are the same as those from past scholars.

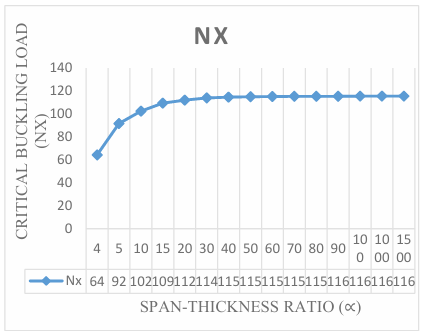
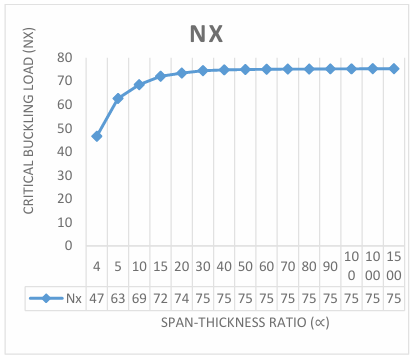
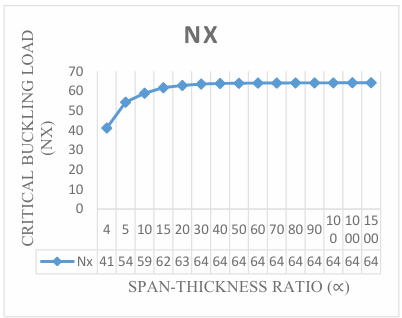
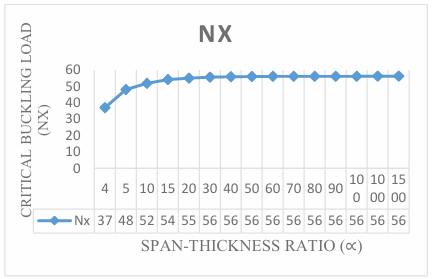
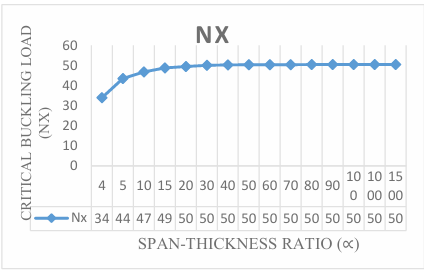
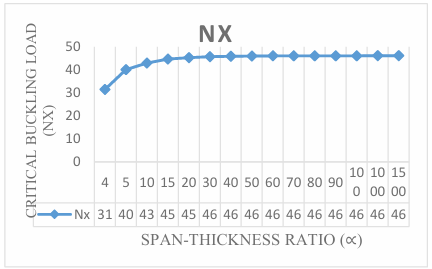
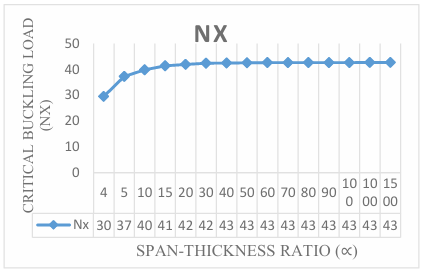
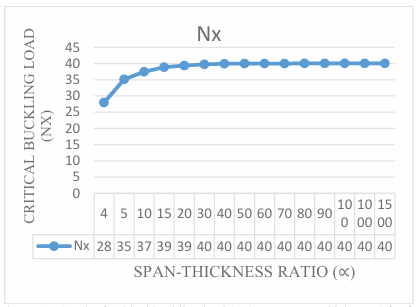
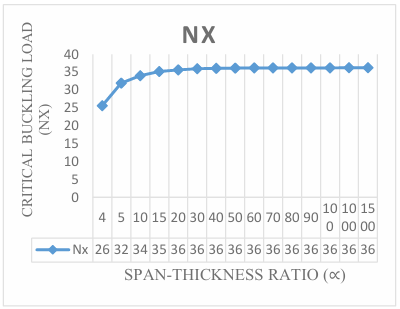
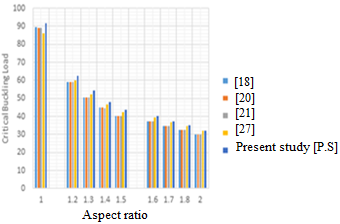
Table 1: Comparison of critical buckling load of plate between the present study [P.S] and previous studies on CCCS plate at span to thickness ratio of 7

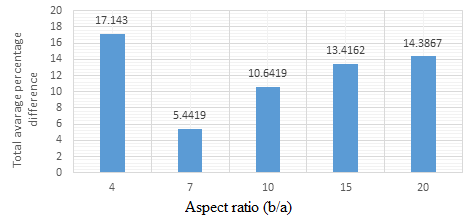
Table 2: Percentage difference analysis between the present study [P.S] and previous studies on CCCS plate at span to thickness ratio of 7

1.  F. C. Onyeka, O. M. Ibearugbulem, “Load Analysis and Bending Solutions of Rectangular Thick Plate,”International Journal of Emerging Technologies, vol. 11, no. 3, pp. 1030-1110, 2020.
2. F. C. Onyeka, T. E. Okeke, “Analysis of Critical Imposed Load of Plate Using Variational Calculus,” Journal of Advances in Science and Engineering, vol. 4, no. 1, pp. 13–23, 2021, doi:10.37121/jase.v4i1.125.
3. F. C. Onyeka, D. Osegbowa, E. E. Arinze, “Application of a New Refined Shear Deformation Theory for the Analysis of Thick Rectangular Plates,” Nigerian Research Journal of Engineering and Environmental Sciences, vol. 5, no. 2, 901-917, 2020.
4. F. C. Onyeka, “Critical Lateral Load Analysis of Rectangular Plate Considering Shear Deformation Effect,” Global Journal of Civil Engineering, vol. 1, pp. 16–27, 2020, doi:10.37516/global.j.civ.eng.2020.0121.
5. K. Shwetha, V. Subrahmanya, P. Bhat, “Comparison between thin plate and thick plate from navier solution using matlab software,” International Research Journal of Engineering and Technology (IRJET), vol. 5, no. 6, pp. 2675 – 2680, 2018.
6. F. C. Onyeka, E. T. Okeke, J. Wasiu, “Strain–Displacement expressions and their effect on the deflection and strength of plate,” Advances in Science, Technology and Engineering Systems, vol. 5, no. 5, pp. 401–413, 2020, doi:10.25046/AJ050551.
7. S. P. Timoshenko, J. M., Gere, W. Prager, Theory of Elastic Stability, Second Edition. In Journal of Applied Mechanics (2nd ed., Vol. 29, Issue 1). McGraw-Hill Books Company, 1962, doi:10.1115/1.3636481.
8. F. C. Onyeka, E. T. Okeke, “Analytical Solution of Thick Rectangular Plate with Clamped and Free Support Boundary Condition using Polynomial Shear Deformation Theory,” Advances in Science, Technology and Engineering Systems Journal, vol. 6, no. 1, pp. 1427–1439, 2021, doi:10.25046/aj0601162.
9. J. N. Reddy, Classical Theory of Plates, In Theory and Analysis of Elastic Plates and Shells, CRC Press, 2006, doi:10.1201/9780849384165-7.
10. D. O, Onwuka, S. E. Iwuoha, “Elastic Instability Analysis Of Biaxially Compressed Flat Rectangular Isotropic All-Round Clamped (CCCC) plates,” MOJ Civil Eng; vol. 2, no. 2, pp. 52‒56, 2017, doi: 10.15406/mojce.2017.02.00027.
11. C. C. Ike, “Kantorovich-Euler Lagrange-Galerkin’s Method for Bending Analysis of thin plates,” Nigerian Journal of Technology (NIJOTECH), vol. 36, no. 2, pp. 351 – 360, 2017, doi: 10.4314/njt.v36i2.5.
12. G. Kirchoff, “Uber das Gleichgewicht und die Bewegung einer elastischen Scheibe. J. Reine Angew,” Math. (Crelle’s J.), vol. 40, pp. 51–88, 1850.
13. E. Reissner,”The Effect of Transverse Shear deformation on the Bending of Elastic Plates,” J. Appl. Mech. Trans. ASME, vol. 12, no. 2, pp. A69–A77, 1945, doi: 10.1115/1.4009435.
14. R. D. Mindlin, “Influence of Rotatory Inertia and Shear on Flexural Motions of Isotropic, Elastic Plates,” J. Appl. Mech. Trans. ASME, vol. 18, no. 1, pp. 31–38, 1951, doi: 10.1115/1.4010217.
15. F. C. Onyeka, B. O. Mama, “Analytical Study of Bending Characteristics of an Elastic Rectangular Plate using Direct Variational Energy Approach with Trigonometric Function,” Emerging Science Journal, vol. 5, no. 6, pp. 916-928, 2021, doi:10.28991/esj-2021-01320.
16. U. G. Eziefula, “Analysis of inelastic buckling of rectangular plates with a free edge using polynomial deflection functions,” International Review of Applied Sciences and Engineering, vol. 11, no. 1, pp. 15-21, 2020, doi:10.1556/1848.2020.00003.
17. I. Shufrin, M. Eisenberger, “Stability and vibration of shear deformable plates – First order and higher order analyses,” International Journal of Solids and Structures, vol. 42, no. (3–4), pp. 1225–1251, 2005, doi:10.1016/j.ijsolstr.2004.06.067.
18. O. M. Ibearugbulem, J. C. Ezeh, U. C. Nwachukwu, “Application of Split – Deflection Method in Buckling Analysis of CCSS and CCCS Thin Rectangular Isotropic Plates under Vibration,” International Journal of Innovative Research and Advanced Studies (IJIRAS), vol. 6, no. 2, pp. 7-12, 2019.
19. O. M. Ibearugbulem, “Using the product of two mutually perpendicular truncated polynomial series as shape function for rectangular plate analysis. International Journal of Emerging Technologies and Engineering (IJETE), 2014 ICRTIET Conference proceeding.
20. E. Ventsel, T. Krauthammer, Thin plates and shells: theory, analysis and applications, 2001, New York: Marcel Dekker.
21. S. Uzoukwu, O. M. Ibearugbulem, C. E. Okere, J. I. Arimanwa, “Stability Analysis of Rectangular CCSS and CCCS Isotropic Plates using 3rd Order Energy Functional,” Global Scientific Journals, vol. 9, no. 1, pp. 637-649, 2021.
22. F. C. Onyeka, F. O. Okafor, H. N. Onah, “Buckling Solution of a Three-Dimensional Clamped Rectangular Thick Plate Using Direct Variational Method,” IOSR Journal of Mechanical and Civil Engineering (IOSR-JMCE), vol. 18, no. 3, pp. 10-22., 2021, doi: 10.9790/1684-803031022.
23. V. T. Ibeabuchi, O. M. Ibearugbulem, C. Ezeah, O. O. Ugwu, “Elastic Buckling Analysis of Uniaxially Compressed CCCC Stiffened Isotropic Plates,” Int. J. of Applied Mechanics and Engineering, vol. 25, no. 4, pp.84-95, 2020, doi: 10.2478/ijame-2020-0051.
24. F. C. Onyeka, B. O. Mama, J. Wasiu, “An Analytical 3-D Modeling Technique of Non-Linear Buckling Behavior of an Axially Compressed Rectangular Plate. International Research Journal of Innovations in Engineering and Technology – IRJIET, vol. 6, no. 1, pp. 91-101, 2022, doi: 10.47001/IRJIET/2022.601017
25. F. C. Onyeka, B. O. Mama, C. D. Nwa-David, “Analytical Modelling of a Three-Dimensional (3D) Rectangular Plate Using the Exact Solution Approach,” IOSR Journal of Mechanical and Civil Engineering (IOSR-JMCE), vol. 11, no. 1, pp. 76-88, 2022, doi: 10.9790/1684-1901017688.
26. A. Moslemi, B. N. Navayi, J. A. Vaseghi, “3-D Elasticity Buckling Solution for Simply Supported Thick Rectangular Plates using Displacement Potential Functions,” Applied Mathematical Modelling, vol. 40, no. 11–12, pp. 5717–5730. 2016, doi:10.1016/j.apm.2015.12.034.
27. F. C. Onyeka, T. E. Okeke, C. D. Nwa-David, “Stability Analysis of a Three-Dimensional Thick Rectangular Isotropic Plates with Arbitrary Clamped and Simply Supported Boundary Conditions,” IOSR Journal of Mechanical and Civil Engineering (IOSR-JMCE), vol. 19, no. 1, Ser. IV, pp. 01-09, 2022, doi: 10.9790/1684-1901040109.
28. F. C. Onyeka, “Direct Analysis of Critical Lateral Load in a Thick Rectangular Plate using Refined Plate Theory,” International Journal of Civil Engineering and Technology, vol. 10, no. 5, pp. 492-505, 2019.

Citations by Dimensions

Citations by PlumX

Crossref Citations

No related articles were found.