It is pertinent to highlight areas POLYMATH software is useful for chemical engineering analysis. Its applications had been demonstrated in this paper using 10 Problem Set, in areas that includes transport phenomena, heat transfer, reaction, and bioreaction kinetics to solve differential equations, nonlinear equations, simultaneous linear equations, graphical representation and regression problems arising in these fields using Licensed POLYMATH Software Version 6.10.261. POLYMATH is mostly used by students, teachers and researchers for educational purposes, but however limited in application by engineers in process industries, as more sophisticated softwares are preferred. Incorporating many solution approaches there in the literature for solving mathematical method problems, especially the newly proposed novel Extended Runge-Kutta Method of Order 6 into POLYMATH and the enabling of log-log plots is hereby recommended.

1. Introduction

Tiring engineering task, including calculations and analysis, today are carried out using computerized systems or specific softwares designed for specific type or large variety of functions. Computers are therefore, powerful tools employed to collect, store, process and analyze data for simulation, explaining mathematical models and analysis of basic scientific phenomena [1]. Chemical engineers employ the services of softwares such as POLYMATH, ASIM, MathCad, AQUASIM, MAPLE, Mathematica, FORTRAN, Excel, MATLAB and ASPEN among others for purposeful analysis. So, the act of finding the root causes of observed phenomenon utilizing both statistical, graphical and numerical analysis softwares is termed chemical engineering analysis. Chemical engineering analysis is thus broadly applied in chemical reaction engineering (CRE), transport phenomena (e.g. fluid mechanics, heat and mass transfer), process dynamics and control, thermodynamics, phase equilibria and distillation and biochemical engineering among others [2]. In CRE, problems solved with POLYMATH are co-current and countercurrent heat exchange, nonlinear regression of rate equations, nonlinear algebraic balances on continuous stirred tank reactors (CSTRs), growth kinetics in bioreactors and membrane reactors, multiple reactions with heat effects, to mention a few [3].

POLYMATH is an educational software recommended for mathematicians, engineers [4] and financial analysts, created by Shacham and Cutlip in January 1, 2003. The challenge of using FORTRAN and C++ is that, a very lengthy time is spent developing and testing codes [3] in addition to hours spent analyzing the result based on different possible scenarios. Unlike ASPEN and COMSOL where the equations behind the computations are hidden, POLYMATH allow the user to provide their mathematical model where necessary [5] and are solved immediately. Errors in the typed mathematical models, entry of wrong initial estimates or the selection of an inappropriate solution algorithm would prevent the software package from given the correct solutions to problems entered [6, 7]. A table of results containing initial estimates, problem statement and calculated unknown parameters are presented by POLYMATH together with graphs relating some of the parameters in the expression [8]. A hardcopy of this result can sometimes be printed by pressing the function key (F3) on the keyboard [9].

Famously, a solution to ten (10) chemical engineering numerical problems that cut across different aspects of chemical engineering, titled (i) molar volume and compressibility factor from Van Der Waal’s equation, (ii) steady state material balances on a separation train, (iii) vapor pressure data representation by polynomials and equations, (iv) reaction equilibrium by multiple gas phase reactions, (v) terminal velocity of falling particles, (vi) unsteady state heat exchange in a series of agitated tanks, (vii) diffusion with chemical reaction in a one dimensional slab, (viii) binary batch distillation, (ix) reversible, exothermic, gas phase reaction in a catalytic reactor, and (x) dynamics of a heated tank with PI temperature control, had been solved using six numerical software packages including Excel, MAPLE, MATHCAD, MATLAB, MATHEMATICA, and POLYMATH [4] for undergraduate education [1]. Statistical analysis of adsorption isotherm models and estimation of growth kinetic parameters can be done using POLYMATH [10, 11]. It is a user friendly software for numerical computation with short learning time, requiring minimal user intervention in technical details of the solution process and had been incorporated into several text, such as Kyle’s textbook of ‘‘Chemical and Process Thermodynamics’’ and Fogler’s textbook of ‘‘Elements of Chemical Reaction Engineering’’ among others [1]. An android application that can run on a minimum of Android 2.2 version called PolyMath Lite had been developed by Cutlip in 2016 [12].

2. Features of POLYMATH Software Package

POLYMATH is a simple software package developed to help students, academicians and engineers

Table 1: Chemical Engineering Problem Set with POLYMATH Solutions [14–17]

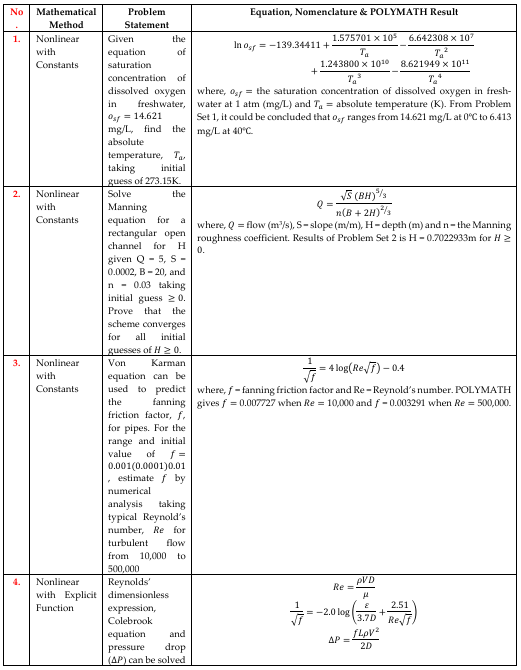
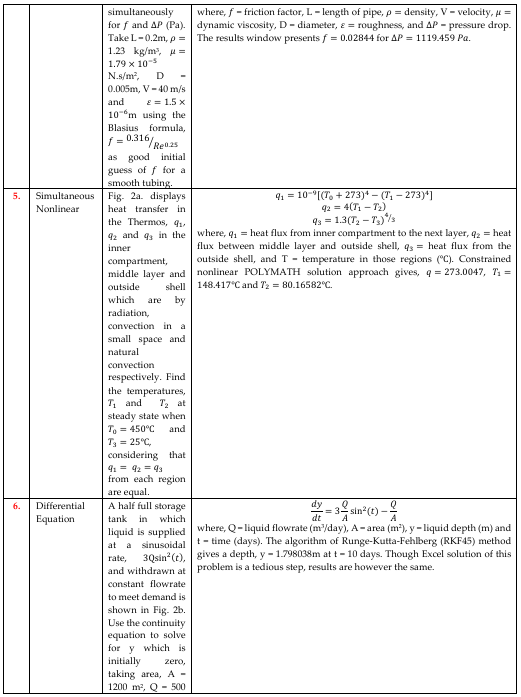
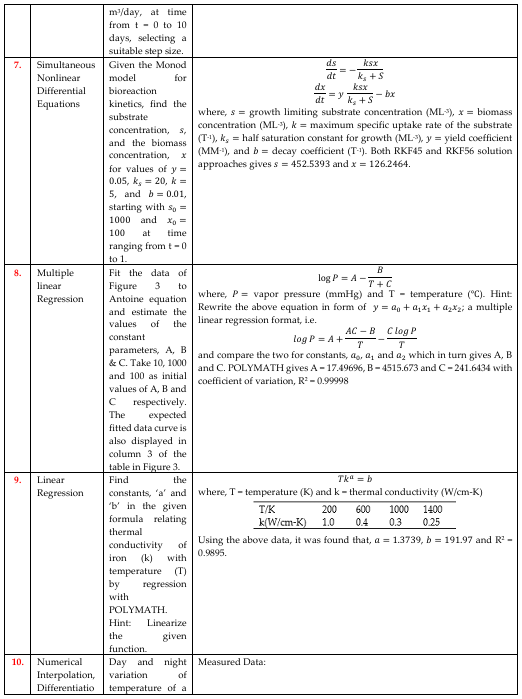
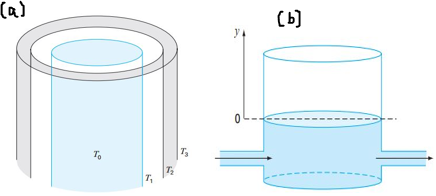
3. Nonlinear Equations

Chemical engineering problems can possibly result in a single or sets of nonlinear equations solvable by numerical methods, including Secant Method, Regula-Falsi, Iterative Method, Bisection, and Newton’s Method. Equations of state (EOS) in Thermodynamic, flow equations in Transport Phenomena (e.g. Manning, Von Karman and Colebrook equations as defined in Problem Set 2-4 of Table 1), equilibrium equation in Separation Processes, and Heat Transfer problems seen in Problem Set 5, to mention a few are solved using any of these methods. In [18], Newton’s algorithm had been applied to formulate a programming codes capable of solving cubic EOS. Among these EOS, [6] demonstrated how Redlich-kwong equation of state is solved using successive substitution method, a method similar to how Problem Set 5 in this work was solved using POLYMATH. In [19], the modified Raoult’s law had been solved using simultaneously with Wilson equation to determine the composition of a non-ideal binary mixture.

In POLYMATH, nonlinear equations are solved with basically two methods: (a) Newton’s, and (b) Broyden’s method. The “safenewt” algorithm uses the Newton’s technique with line search to guarantee reduction of the norm of the function values in all iteration [20]. Broyden is a quasi-Newton method (or the generalization of the Secant method to nonlinear systems) that is superlinearly convergent for finding roots in k variables, as it reduces the amount of calculation at each iteration without significantly degrading the speed of convergence [21]. Therefore, both ‘safenewt’ and ‘safebroyd’ includes function minimization along the Newton and Broyden directions.

4. Differential Equations

POLYMATH would request the typing of a function to be solved by numerical methods or user-defined functions to be entered for regression purposes. Functions generate one unique output for each input [8] which are termed as arguments, often enclosed in parenthesis [9]. Some of the functions recognized by POLYMATH are ‘sin’, ‘sinh’, ‘cos’, ‘cosh’, ‘tan’, ‘tanh’, ‘ln’, ‘log’, ‘arcsin’, ‘arccos’, ‘arctan’, ‘exp’, ‘frac’, ‘int’, ‘abs’, ‘sign’, and ‘round’. For example, absolute value of say ‘x’ can be written as “abs(x)”. Also, factorial of an integer, say ‘5’ is written as “5!” in POLYMATH. Differential functions which are implicit type of functions as well as explicit functions must be specified in POLYMATH.

Differential equations are classified into ordinary or partial differential equations and linear or nonlinear equations [22]. A mathematical equation that relates some functions with their derivatives are known as differential equations. Practically, the functions represent physical quantities, the derivatives stand for their rates of change, and the equation defines a relationship between the two [8]. Modeling of the variation of a physical quantity, such as temperature, pressure, displacement, velocity, stress, strain, current, voltage, or concentration of a pollutant, with the change of time or location, or both would result in differential equations [23].  Differential equation govern almost all physical processes of interest to chemical engineers, namely [24]; description of thermodynamic laws, description of flow processes (e.g. using Darcy’s law, Bernoulli’s equation, Nervier-Stoke and mass conservation equations), microbial growth kinetic constant estimation, representation of reaction rates in CRE, Fick’s law of diffusion in mass transfer and many more. Elsewhere, [25] highlighted some of the applications of ODEs in reaction engineering. Partial differential equations (PDEs) on the other hand, finds applications in CRE to model complex reactors and reacting systems [3]. Important examples of PDEs are, Tricomi equation, Laplace equation, Helmholtz equation, Poisson-Boltzmann equation, Lorenz equations, Cauchy-Riemann equations, Poisson’s equation, Plate bending, Schrdinger’s equation, Geodesic equation, Navier-Stokes, Wave equation (1D-3D) and Fourier equation [22, 23]. Softwares that can deal with PDEs are COMSOL (formerly FEMLAB) and MATLAB, especially for reactions taking place in tubular reactors [3]. ODEs in Problem Set 6 & 7 where solved by POLYMATH which is also utilizing the six parameters of the RKF method in equations (1) [26, 27].

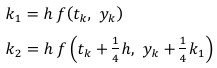
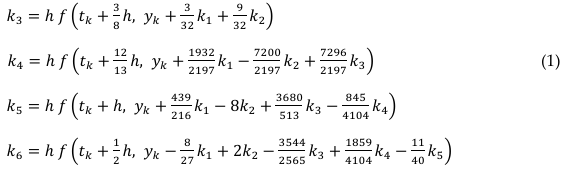
An approximate solution, to given initial value problems (IVPs) can then be executed using the RKF45 approximation as in equation (2):

An improved value of the solution, is determined using another approximation. Check equation (3):

Note that the approximations in (2) and (3) of the RKF45 method [26] ignores,  This makes equation (2) of order 4 and (3), an order 5 equation; basically, making use of the classical Runge-Kutta methods of order 4 and 5 together, therefore defining RKF45 algorithm holistically. The selection of appropriate step sizes, h, guarantees the accuracy of most IVPs. The advantage of the RKF45 algorithm is that, it ensures that the right, h is used on its own and not allowing the user to specify any step size. Problem Set 6 had been coded to give, using a step size of h = 0.1 for the RKF45 technique using C++ as seen in the Appendix. RKF56 on the other hand is termed the 6th order Runge-Kutta-Fehlberg method and is presented by [28]. The Runge-Kutta-Fehlberg method is generally thought of as one of the best methods existing for solving non-stiff systems of equations [27].

Starting from order 1 to 6, differential equations are solved using (i) Euler’s method of order 1, (ii) Heun’s method (or modified Euler or leap-frog formula) of order 2, (iii) Bogacki-Shampine method of order 3, (iv) Runge-Kutta method of order 4, (iv) R-K-Fehlberg method of order 4 with an error estimator of order 5 (RKF45), and (v) RKF method of order 5 with an error estimator of order 6 (RKF56). Beyond this, not long ago, [29] proposed a novel Extended RK 6th order method to bring the number of the solution approaches to six. A differential equation of the form,  is said to be stiff if its exact solution includes a term that decays exponentially to zero as  increases (i.e. , where c is a large positive constant), but whose derivatives are much greater in magnitude than the term itself [30]. A stiff differential equation is further characterized as being numerically unstable unless the step size is extremely small [30]. Stiff and Burlirsch-Stoer (BS) are alternative solution techniques similar to Runge-Kutta.

5. Data Regression

The most extensively used statistical technique is regression analysis, which involves detecting, evaluating, and analyzing the connection between the dependent and independent variables [31]. As mentioned earlier, the regression window in POLYMATH is divided into 3 tabs, namely, ‘Regression’, ‘Analysis’ and the ‘Graph’ tab. User-defined linear and multiple linear regression was carried out in Problem Set 8 and 9 to determine unknown constants, however, using the nonlinear function definition provided by POLYMATH. Regressed graph of the calculated and experimental data of Problem 8 is shown in Figure 3.

In chemical engineering, regression tools are widely used to determine unknown constant parameters in Arrhenius equation, Antoine equation, microbial growth models, EOS parameters, rate equations, biogas kinetic models and many other proposed models in the literature. KaleidaGraph program (Synergy software), PAST, SigmaPlot, SAS, EViews, GraphPad Prism, SPSS, Matrixer, SHAZAM, Statistica, ORIGINPro, Datafit, JASP, PSPP, Xlstat Excel Add-in, Excel Solver, Jamovi, Minitab, Stata, KyPlot, Scilab, nonlinear curve fitting toolbox of MATLAB and NCSS are competitive softwares for regression analysis apart from POLYMATH [32, 33].

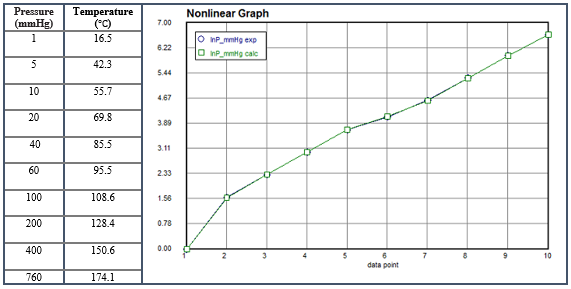
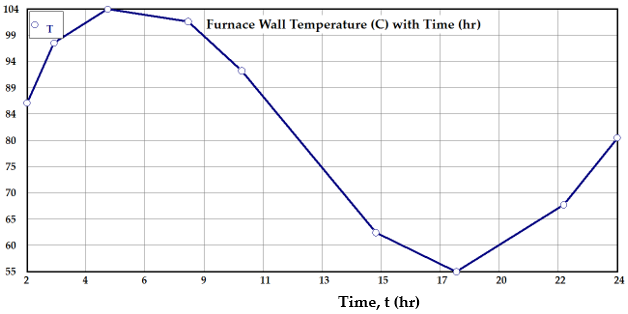
We have demonstrated how to use POLYMATH to carryout numerical differentiation, interpolation, integration as well as data plots for Problem Set 10. Interpolation, formerly can be described as a method of estimating missing data values that are in-between a given set of field data [34]. Typical example is approximating of function values (e.g. temperature) in heat transfer and/or thermodynamics at points where there is no data reading and when computing derivatives from empirical data values.

In chemical engineering, regression tools are widely used to determine unknown constant parameters in Arrhenius equation, Antoine equation, microbial growth models, EOS parameters, rate equations, biogas kinetic models and many other proposed models in the literature. KaleidaGraph program (Synergy software), PAST, SigmaPlot, SAS, EViews, GraphPad Prism, SPSS, Matrixer, SHAZAM, Statistica, ORIGINPro, Datafit, JASP, PSPP, Xlstat Excel Add-in, Excel Solver, Jamovi, Minitab, Stata, KyPlot, Scilab, nonlinear curve fitting toolbox of MATLAB and NCSS are competitive softwares for regression analysis apart from POLYMATH [32, 33]. We have demonstrated how to use POLYMATH to carryout numerical differentiation, interpolation, integration as well as data plots for Problem Set 10. Interpolation, formerly can be described as a method of estimating missing data values that are in-between a given set of field data [34]. Typical example is approximating of function values (e.g. temperature) in heat transfer and/or thermodynamics at points where there is no data reading and when computing derivatives from empirical data values.

To show how one quantity vary with another related quantity, graphs are readily used to convey information to readers than if same information are explained in words [35]. Graphs can also be plotted in POLYMATH just like Excel as depicted in Figure 1. However, POLYMATH cannot be used to plot a log-log scale. Log-log graphs is a scatterplot in which both axes have a logarithmic scale [36]. A log-log plot displays the relationship, such as one in Problem Set 9 as a straight-line equivalent to The Bode plot, a graphical depiction of the frequency responses of a system in control and electrical engineering is a log-log plot [37]. The idea behind this type of plot according to [36] is to use the axes so we can more easily see details for small and large values of the dependent variable, and to show % change or multiplicative factors. Log-log scales are plotted very easily in Excel for an existing scatter plot by clicking on the “Logarithmic Scale” check box under Format Axis after right-clicking on the values along the x-axis. This is then repeated for the y-axis.

6. Linear Equations

Not one, but sets of simultaneous linear equations are solved using numerical analysis softwares. Methods of solution are usually, Cramer’s rule, substitution method, elimination method [35], graphical, and adjoint method which requires painstaking steps if the number of equations is more than 3. The fastest tool of solving a system of simultaneous linear equations is POLYMATH. In chemical engineering, simultaneous equations are used to balance chemical equations, finding unknowns in material balances, constrained optimization problems of differential equations after applying Laplace transform, solving certain functional equations among others. In real life, a smartphone user can use system of linear equations to select, best cell phone data plan knowing the charge rate of different companies per minute [38]. Also, to determine if one will make more money at one job or another, taking multiple variables (e.g. salary, benefits and commissions) into account [38]. POLYMATH cannot solve sets of linear inequality constraint equations used in cost optimization in chemical plants [39].

7. Conclusion

POLYMATH provisions for solutions to numerical problems makes it a useful chemical engineering analysis tool. An Android application called PolyMathLite had been created to further go into user’s smart phones. The software package is limited to not possessing the features for solving PDEs in engineering. Unlike Excel, Tora, Lingo and sometimes C++ programs, it cannot solve linear programming problems, involving cost minimization or maximization in chemical plants. POLYMATH has the advantage of solving ODEs by selecting the best step size necessary while the use of programming codes would take much time and lengthy iterations before arriving at a solution and sometimes crash a system if ‘h’ is very negligible.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgement

The authors acknowledge the support given by Federal University Wukari as well as the University of Maiduguri.

1. A. Brenner, M. Shacham, M. B. Cutlip, “Applications of mathematical software packages for modelling and simulations in environmental engineering education,” Environmental Modelling & Software, vol. 20, pp. 1307–1313, 2005, doi:10.1016/j.envsoft.2004.09.007.
2. M. B. Cutlip, M. Shacham, Problem solving in chemical and biochemical engineering with POLYMATH, Excel, and MATLAB, 2nd ed. (Prentice Hall International Series, 2008).
3. H. S. Fogler, M. B. Cutlip, “Chemical Reaction Engineering (CRE) education: From the era of slide rule to the digital age.” www.fdcocuments/in . (accessed: 30-Sep-2021).
4. M. B. Cutlip, M. Shacham, “Polymath solutions to the chemical engineering demonstration problem set.” .
5. R. Hesketh, “Application of numerical problem solving in chemical engineering coursework,” ASEE 2017 Chemical Engineering Summer School, pp. 1–6, 2017.
6. M. Shacham, N. Brauner, “Solving a system of nonlinear algebraic equations: You only get error messages-What to do next?,” Checmial Engineering Education, vol. 15, no. 2, pp. 75–82, 2017.
7. M. Shacham et al., “Can I trust this software package? An excercise in validation of computational results,” Checmial Engineering Education, vol. 42, no. 1, pp. 53–59, 2008.
8. Hashim Khan, “Polymath tutorial for Chemical Engineers.” : 1–4, 2005.
9. M. Schacham, M. B. Cutlip, “User-Friendly numerical analysis programs.” http://www.polymath-software.com . (accessed: 27-Sep-2021).
10. G. K. Rajahmundry et al., Statistical analysis of adsorption isotherm models and its appropriate selection, vol. 276, (2021).
11. A. M. Abubakar, Z. Soltanifar, M. M. Kida, Sensitivity analysis of kinetic growth model data: Monod equation (Revista Rebibio, 2022).
12. M. B. Cutlip, “Enabling extensive numerical problem solving on smartphones and tablets,” ASEE International Forum, pp. 1–10, 2014.
13. F. J. Keil, “Application of numerical methods in chemical process engineering,” Scientific Computing in Chemical Engineering, pp. 1–19, 1996, doi:10.1007/978-3-642-80149-5_11.
14. V. J. Law, Numerical methods for Chemical Engineers using Excel, VBA, and MATLAB (New York: CRC Press, 2013).
15. S. C. Chapra, R. P. Canale, Numerical methods for engineers, 6th ed. (New York, United States: McGraw Hill Companies, 2020).
16. CheGuide, “Curve fitting data to an Antoine equation-A guide for Chemical Engineers working in process industry,” in Chemical Engineer’s Guide (CheGuide), (2015).
17. UMD, “Regression practice problems,” in Practical Numerical Methods, (University of Minnesota Duluth, 2021), 30–36.
18. A. M. Abubakar, A. A. Mustapha, “Newton’s method cubic equation of state C++ source code for iterative volume computation,” SSRG International Journal of Recent Engineering Science, vol. 8, no. 3, pp. 12–22, 2021, doi:10.14445/23497157/IJRES-V8I3P103.
19. J. G. Eberhart, “Solving nonlinear simulatneous equations by the method of successive substitution: Applications to equations of state,” Journal of Chemistry Education, vol. 71, no. 12, pp. 1038–1040, 1994, doi:https://doi.org/10.1021/ed071p1038.
20. W H Press et al., “Attempting to solve the systems of equations,” in Numerical Recipes, 2nd ed. , (Cambridge, United States: Cambridge University Press, 1992), 40.
21. A. Ramli, M. L. Abdullah, M. Mamat, Broyden’s method for solving Fuzzy nonlinear equations (Hindawi, 2010).
22. Cheng Yung Ming, “Solution of differential equations with applications to engineering problems,” (IntechOpen, 2017), 33, doi:http://dx.doi.org/10.5772/67539.
23. B. Sumithra, “Engineering applications of differential equations,” International Journal of Application or Innovation in Engineering & Management (IJAIEM), vol. 6, no. 7, pp. 110–114, 2017.
24. P Rees, O Kryvchenkova, and P D Ledger, “Engineering Analysis 2: Ordinary Differential Equations.” College of Engineering, Swansea University, United Kingdom, : 1–37, 2017.
25. C. B. Mohod, “Application of Ordinary Differential Equations (ODEs) in reaction engineering: Review,” International Journal of Chemical and Molecular Engineering, vol. 2, no. 1, pp. 1–9, 2016.
26. John H Mathews and Kurtis K Fink, “Runge-Kutta Methods,” in Numerical Methods Using Matlab, 4th ed. , (New Jersey: Prentice-Hall Inc, 2004), 497–499.
27. C. F. Mayo, “Implementation of the Runge-Kutta-Fehlberg method for solution of ordinary differential equations on a parallel processor,” (Naval Postgraduate School (NPS)-Dudley Knox Library, 1987).
28. L. Derr, C. Outlaw, D. Sarafyan, “A new method for derivation of continuous Runge-Kutta formulas,” Computers Math. Application, vol. 26, no. 3, pp. 7–13, 1993.
29. W. Suryaningrat, R. Ashgi, S. Purwani, “Order Runge-Kutta with extended formulation for solving ordinary differential equations,” International Journal of Global Operations Research (IJGOR), vol. 1, no. 4, pp. 160–167, 2020.
30. Jim Lambers, “Stiff differential equations: Lecture 9 notes,” in MAT 461/561, (2010), 1–4.
31. J. O. Rawlings, S. G. Pantula, D. A. Dickey, Applied regression analysis: A research tool, 2nd ed. (Carolina, USA: Springer, 1998).
32. J. Tellinghuisen, “Using least squares to solve systems of equations.” Tennessee, USA, 2015.
33. P. Rani et al., Experimental and kinetic studies on co-digestion of agrifood and sewage sludge for biogas production, vol. 16, no. 1, (Taylor and Francis Group, 2022).
34. C. R. Chikwendu, H. K. Oduwole, S. I. Okoro, An application of sline and piecewise interpolation to heat transfer (cubic case), vol. 5, no. 6, (IISTE Knowledge Sharing Partners, 2015).
35. J. Bird, Basic engineering mathematics, 5th ed. (United Kingdom: Elsevier Ltd, 2010).
36. M. Bourne, “Graphs on logarithmic and semi-logarithmic axes.” https://www.intmath.com/exponential-logarithmic-functions/7-graphs-log-semilog.php . (accessed: 06-Oct-2021).
37. Y. Bavafa-Toosi, “Introduction to linear control systems,” SIAM Review, vol. 61, no. 1, pp. 209–225, 2019, doi:https://doi.org/10.1137/19N974750.
38. M. H. Snyder, “10 ways simultaneous equations can be used in everyday life.” www.sciencing.com/10-can-used-everyday-life-8710568.html . (accessed: 04-Oct-2021).
39. A. M. Abubakar et al., “Simplex C++ syntax for solving chemical engineering cost optimization problems,” Research Inventy: International Journal of Engineering And Science, vol. 11, no. 7, pp. 39–47, 2021, doi:10.5281/zenodo.5146856.

Citations by Dimensions

Citations by PlumX

Crossref Citations

1. Abdulhalim Musa Abubakar, Bello Iliyasu, Zakiyyu Muhammad Sarkinbaka, “Enterprise-Grade CI/CD Pipelines for Mixed Java Versio Environments Using Jenkins in Non-Containerized Environments”, Journal of Engineering Research and Sciences, vol. 4, no. 9, pp. 12–21, 2025. doi: 10.55708/js0409002
2. Abdulhalim Musa Abubakar, Bello Iliyasu, Zakiyyu Muhammad Sarkinbaka, “Analysis of Difference Schemes of Two-Point Boundary Value Problems using the Method of Moving Nodes”, Journal of Engineering Research and Sciences, vol. 4, no. 6, pp. 9–15, 2025. doi: 10.55708/js0406002
3. Abdulhalim Musa Abubakar, Bello Iliyasu, Zakiyyu Muhammad Sarkinbaka, “Analysis of 5G Business Model Components for Mobile Network Operators in Sub-Saharan Africa”, Journal of Engineering Research and Sciences, vol. 4, no. 2, pp. 1–10, 2025. doi: 10.55708/js0402001
4. Abdulhalim Musa Abubakar, Bello Iliyasu, Zakiyyu Muhammad Sarkinbaka, “Enhancing Python Code Embeddings: Fusion of Code2vec with Large Language Models”, Journal of Engineering Research and Sciences, vol. 4, no. 1, pp. 1–7, 2025. doi: 10.55708/js0401001
5. Abdulhalim Musa Abubakar, Bello Iliyasu, Zakiyyu Muhammad Sarkinbaka, “Smart Vehicle Safety System Using Arduino: An Experimental Study in Bahrain’s Driving Conditions “, Journal of Engineering Research and Sciences, vol. 3, no. 11, pp. 74–80, 2024. doi: 10.55708/js0311006