Estimating the natural voluntary movement of human joints in its entirety is a challenging problem especially when high accuracy is desired. In this paper, we build a modular estimator to estimate the elbow joint motion including angular displacement and direction. Being modular, this estimator can be scaled for application to other joints. We collected surface Electromyographic (sEMG) signals and motion capture data from healthy participants while performing elbow flexion and extension in different arm positions and at different effort levels. We preprocessed the sEMG signals, extracted features array, and used it to train an ANN-based Softmax classifier to estimate the angular displacement and movement direction. When compared against the motion cap-ture data, the classifier achieved estimation accuracy ranging from 80% to 90% with a resolution of 5°, which translates into Pear-son Correlation Coefficient (PCC) ranging from 0.91 to 0.95. Such high PCC values in mimicking the voluntary movement of the upper limb may help toward building intuitive prostheses, exoskeletons, remote-controlled robotic arms, and other Human Ma-chine Interface (HMI) applications.

1. Introduction and Literature Review

An Individual’s intent to perform any physical movement that involves the contraction of skeletal muscles can be estimated by analyzing the corresponding muscles’ electromyography (EMG) signal [1,2]. An EMG signal is the electrical manifestation of the neuromuscular activation associated with a muscle contraction [3]. EMG signals are characterized as a stochastic and nonlinear signal due to a large number of motor units and their different firing rates, as it carries the brain command to create a muscle contraction [4]. Since the EMG signal has a low signal-to-noise ratio in addition to its stochastic nature, it is hard to fully utilize the information embedded in it with high accuracy without implementing various filtering, dimension reduction, and/or pattern recognition techniques [4,5]. EMG can be measured by using one of two methods; surface EMG or sEMG and intramuscular EMG. sEMG is measured on the skin above the muscle of interest using an electrode to measure the muscle’s electrical activity i.e. EMG signal [6]; therefore, this technique is categorized as noninvasive [6,7]. Intramuscular EMG, on the other hand, is measured from within the muscle of interest by inserting thin metal electrodes into the muscle and referenced to the surface electrode placed above the muscle [8]. Consequently, it requires more caution than sEMG to perform and it is considered an invasive procedure [9,10]. As a result, sEMG is the dominant method to study how the human body controls skeletal muscles as it is safer, easier to perform, and can be implemented in end products with less complexity [7,10].

This work focuses on estimating the direction and angular displacement of the elbow’s joint flexion and extension movement using the information embedded within sEMG data of the related muscles. Below we mention some of the related research addressing the same problem using various methods. The authors trained an Artificial Neural Network (ANN) to estimate the upper limb joint angles from related muscles’ sEMG data, in their experiment setup the upper arm was held fixed at the shoulder level [11]. Their ANN was able to follow the target angle in training data, and they showed low average Mean Square Error (MSE) for eight participants. The authors measured the upper limb joint angles, muscles EMG and set a constant load to estimate the angle-torque relation during constant muscle activation in able-bodied humans using ANN [12]. The authors showed the effectiveness of Kalman Filter in linearizing a set of twelve time-domain features. They estimated the elbow joint angle during elbow flexion with a fixed load and position which in turn increased the elbow angle estimation accuracy [13]. The authors used least squares support vector regression to estimate the knee and hip joint angles using sEMG signals [14]. Their data was from able-bodied participants performing treadmill and leg extension exercises. They were able to achieve single-digit Root Mean Square Error (RMSE) between measured and estimated joint angles in training data. The authors were able to estimate the elbow joint angle in able-bodied participants, using multiple time-delayed features of the sEMG and random forests [15]. They were able to achieve single-digit MSE but they had a fixed time window, with strictly one degree of freedom, fixed arm effort, and fixed arm orientation. The same authors from [15] used grey feature weighted least square support vector machine algorithm to estimate the elbow joint angle [16]. Similar to [15], the estimation was for one degree of freedom while the elbow was fixed on the table, and the starting angle between the forearm and the upper arm was 90°and the wrist joint was kept along the forearm and again all the movements were done with empty hand i.e. single effort level. The authors used EMG to model muscle activation with the help of a feed-forward ANN and Gaussian process to estimate the fingers’ joint angles of ten able-bodied participants [17]. Their estimation involved more than one degree of freedom, but was held constant at one effort level. The authors used Radial Basis Function ANN to estimate the elbow joint angle for a flexion and extension movement in healthy participants [18]. Their experimental setup included fixed elbow location, fixed elbow orientation, and a fixed effort level. They achieved correlation coefficient values between actual and estimated angle ranging from 0.76 to 0.91 depending on the movement speed.

The above literature review shows that most, if not all, of the related research, did not account for the following factors when trying to estimate the elbow’s joint movement:

1. Different limb orientation when performing the movement
2. Carried load changes between trials of the same movement
3. Movement speed variation between trials

Therefore, the goal of this work is to estimate the human elbow joint displacement and direction using sEMG signals for one degree of freedom at two different limb orientations, two different load levels, and variable movement speed, thus expanding on the previously mentioned studies. By developing such a versatile joint angle estimator, we broaden the utilization of sEMG signal data in different Human Machine Interface (HMI) application. For an instant prosthesis development has, in a way, surpassed the current limb action estimation techniques; as modern prostheses have multiple degrees of freedom, actuated by motors capable of fine movements [19], while the majority of the cur-rent literature focuses on the estimation of the limb torque during a muscle contraction and not so on the final location of the limb [19–21]. The estimator developed in this work is designed with a modular approach from the software point of view; so it can be scaled to other joints and their corresponding muscle groups, e.g., the wrist or the shoulder.

2. Elbow Joint Movement Estimation

In this section, we describe the biomechanics of the elbow joint and which muscles to focus on to estimate the elbow flexion and extension movement, we also discuss the sEMG signal characteristics and the procedure used in collecting sEMG data for this study. Then we show the methods used to preprocess this data and the building blocks of the elbow angle estimator, and by the end of this section, we show the estimation results of the developed estimator and the correlation factor between the actual and estimated elbow angles. 

2.1. Elbow Joint Anatomy and Biomechanics

Healthy humans take their elbow joint function for granted, but as researchers try to tackle this joint, they realize how complicated this joint is. The elbow joint consists of and is a pathway to a lot of different types of bone structures, tissues, vessels, and fibers [22,23], however in this work we are focusing on the muscles responsible for flexing and extending the joint which can be divided into two groups [23].

1. The prime movers and heavy lifters of the forearm are [23]:
   1. Biceps                 (Elbow Flexion)
   2. Brachialis                 (Elbow Flexion)
   3. Triceps                 (Elbow Extension)
2. The secondary movers and supporting muscles are [23]:
3. Brachioradialis                 (Elbow Flexion)
4. Pronator teres                 (Elbow Flexion)
5. Anconeus                 (Elbow Extension)

The location of the three heavy lifting muscles in number 1 above with respect to the upper limb is shown in Figure 1 [22].

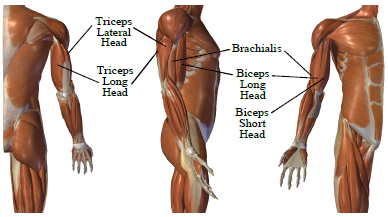
What is interesting is that the body utilizes the elbow muscles in a selective, highly case-dependent manner [22]. For unconstraint and unloaded forearm moving at medium speed, and when the arm is on the side of a standing hu-man, biceps, and brachialis are mainly used to raise and lower the arm, and triceps is mainly used to stabilize the elbow. This movement is known as biceps curls. And the opposite is true when the hand is raised above the shoulder and the arm is extended to the top. In this case, the triceps is mainly used to extend the arm, biceps and brachialis are used to stabilize the elbow, this movement is known as triceps extension [23].

2.2. sEMG Signal Limitations

Many researchers agree that sEMG is the most common and most feasible way to study limbs’ movements and to control prosthetic limbs [24]. Nevertheless, getting useful data from the stochastic sEMG signal has its own challenges [25]. Common disadvantageous characteristics and noise sources of sEMG signal are [26–30]:

1. sEMG signal is Quasi-Random in nature
2. High noise to signal ratio (NSR)
3. Cross-talk noise, which can be mitigated by using smaller footprint sensors and by accurately targeting the muscles in question
4. Inherent equipment and electrode noise (can be estimated to a certain degree from resting trials of sEMG data re-cording session)
5. Inherent electromagnetic noise from the environment e.g. electric power, (part of which can be figured out from the power line frequency, 60 Hz in the USA)
6. Motion artifact noise (usually high amplitude, comparable to sEMG signal and low frequency 1-10 Hz)
7. Heartbeat artifact noise, which is usually very consistent with Electrocardiographic (ECG) signal.
8. Other biological noise sources, e.g. blood flow velocity, fat index, and skin temperature.
9. Fatigue resulting from task repetition and/or increasing the load has its toll on the sEMG signal.
10. sEMG signal distribution is highly non-Gaussian at low and high levels of force, whereas the distribution has its maximum gaussianity at the mid-level of maximum voluntary contraction (MVC). Therefore some techniques may work well at certain levels of the contraction power and fail at different levels [28].

It is obvious that most of the above-mentioned drawbacks are biological noises, some of which can be dealt with using different kinds of filters, and others will need different approaches to get more accurate data from the sEMG.

2.3. Data Collection

Since we can reflect the sEMG signal processing and classification from able-bodied to amputees with not much loss of accuracy [31,32], in this study we will only collect data from volunteer able-bodied participants. The data collection was done in accordance with the Institutional Review Board (IRB) guidelines. Our study was approved by IRB with protocol number 18-134-R1. After describing the whole procedure to the volunteers and signing the consent form, four silver/silver chloride (Ag/AgCl) electrodes were put on the muscles responsible for flexing and extending the elbow joint. The first channel was assigned to the biceps between the long-head and short-head, the second to brachialis, the third to triceps lateral, and the fourth and last channel was assigned to triceps long head. Retro-reflective markers were placed on the right arm of the participants to utilize the Vicon motion capture system to measure the elbow joint angular displacement. Noraxon TeleMyo Direct Transmission System (Noraxon  USA Inc)  was used to record the sEMG and motion data. The sEMG sampling frequency was set to 1500 Hz. Each participant was asked to perform fifteen arm flexing and extension movements at their own pace in three different arm positions:

1. The arm is relaxed by the participant side, a.k.a biceps curl movement
2. The arm abducted to shoulder height to the side of the participant, in which the elbow flexes and extends in the horizontal plane, perpendicular to the gravitational force.
3. Arm above the shoulder, i.e. overhead arm extension movement a.k.a triceps extension.

All three of the above movements were done with an empty hand and while holding a 5-pound weight (two effort levels). We also recorded sEMG data for each arm position while it’s idle i.e., with no movement. Each trial lasted approximately 20 seconds which is the average time the participants took to complete 15 repetitions.

We allocate 80% of the acquired data for training the classifier and 20% for testing it. We also implement a five-fold cross-validation method on the whole data to verify the effectiveness of the classifier across all sections of the data.

2.4. Signal Preprocessing

As mentioned in Section ‎2.2, sEMG signal suffer from different kinds of noise; to address some of these signal imperfections, preprocessing is a must to obtain useful information out of the signal. In this case, we have implemented the following:

1. Removal of DC bias.
2. Notch filters to filter out power line fundamental and harmonic frequencies.
3. Bandpass filter allowing frequencies ranging from 30-400Hz to pass and has a low band stop frequency of 25Hz and a high band stop frequency of 450Hz.
4. Scaling up the signal by a factor of two.

2.5. Elbow Joint Motion Estimator

In this section, we design the estimator which will estimate the elbow joint’s angular displacement magnitude in degrees, as well as its movement direction. Furthermore, it needs to do so while being insensitive to the elbow’s angu-lar speed, orientation, or load changes.

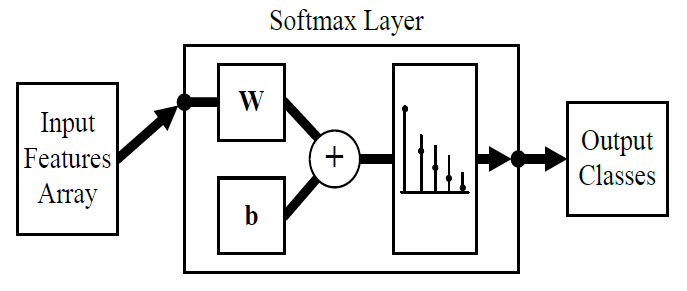
The designed estimator is a classifier at its core, and to be more specific it is an ANN-based Softmax classifier. The softmax function is shown in (1) [33]:

$$P(c_r|\mathbf{x}) = \left\{ \begin{array}{ll}
\frac{P(\mathbf{x}|c_r)P(c_r)}{\sum_{j=1}^{k} P(\mathbf{x}|c_j)P(c_j)}, & \text{(General Form)} \\
\frac{e^{a_r}}{\sum_{j=1}^{k} e^{a_j}}, & \text{(Normalized Exponential form)}
\end{array} \right. \tag{1}$$

Where

\(a_r = \ln\left(P(x|c_r)P(c_r)\right)\)

\(P(x \mid c_r)\) is the conditional probability of the sample  given class  and it has to satisfy the following two conditions:

\(0 \leq P(c_r \mid x) \leq 1 , \quad \sum_{j=1}^{k} P(c_j \mid x) = 1\)

𝑃(𝑐_𝑟) is the class prior probability and the ANN is trained using the scaled conjugate gradient algorithm, [34] provides an elaborate explanation on this algorithm. The selected loss function for this training is cross-entropy which is given in (2) [33]:

$$E = -\frac{1}{n} \sum_{i=1}^{n} \sum_{j=1}^{k} t_{ij} \ln(y_{ij}) + (1 – t_{ij}) \ln(1 – y_{ij})\tag{2}$$

Where

𝐸 is the loss function

𝑁 is the number of samples

𝐾 is the number of classes

𝑡_𝑖,𝑗 means the 𝑖^𝑡ℎ sample belongs to the 𝑗^𝑡ℎ class

𝑦_𝑖,𝑗 is ANN response for sample 𝑖 for class 𝑗

As mentioned in section 2.2 sEMG has some random properties and inherited noises associated with it; thus, before feeding the sEMG data to the estimator it needs to undergo a feature extraction process. This process serves two key purposes:

1. Dimension reduction and normalization.
2. Amplify useful data and suppress noises.

Then the classifier will use the extracted features array instead of the sEMG data to do the classification.

We have chosen the following time-domain features:

1. Mean Absolute Value; \(MAV = \frac{1}{N} \sum_{n=1}^{N} \left| x_n \right|\)
2. Number of Zero Crossings; \(NZC = \sum_{n=1}^{N-1} s(x_i, x_{i+1})\) $$\text{Where } s(x, y) = \begin{cases} 1 & \text{if } (x \cdot y) < 0 \\ 0 & \text{if } (x \cdot y) \geq 0 \end{cases}$$
3. Number of Slope Sign Changes; 𝑆𝑆C = \(\sum_{n=2}^{N-1} ss(Sl_i, Sl_{i+1})
   \) $$\text{Where } ss(x,y) = \begin{cases} 1 & \text{if } (x \cdot y) < 0 \\ 0 & \text{if } (x \cdot y) \geq 0 \end{cases} \quad \text{and} \quad Sl_i = \frac{y_i – y_{i-1}}{x_i – x_{i-1}}$$
4. Root Mean Square Value; \(RMS = \sqrt{\frac{1}{N} \sum_{n=1}^{N} x_n^2}\)
5. Variance within each Channel; \(ChVar = \frac{1}{N – 1} \sum_{n=1}^{N} \left| x_n – \mu \right|^2\) $$\text{Where } \mu = \frac{1}{N} \sum_{n=1}^{N} x_n$$
6. Variance Across Channels; AChVar = \(\frac{1}{nCh – 1} \sum_{n=1}^{nCh} \left| x_{Ch_n} – \mu \right|^2
   \) $$\text{Where } \mu = \frac{1}{nCh} \sum_{n=1}^{nCh} x_{Ch_n}$$
7. RMS Difference between Agonist (Ag) and Antagonist (Antg) Muscles; RMS_Diff = \(\sum_{n=1}^{N^{Ag}} RMS_n -\) \(\sum_{n=1}^{N^{Antg}} RMS_n 
   \)
8. Integration of absolute value of sEMG; 𝐼|EMG |= \(\sum_{n=1}^{N} |x_n| \cdot t_s\) $$\text{Where: } t_s = \frac{1}{sF} \;;\; sF \text{ is the sampling frequency}$$
9. Signal Power; \(SP = \frac{\lVert x \rVert^2}{N}\) $$\text{Where } \lVert x \rVert = \sqrt{x_1^2 + x_2^2 + \cdots + x_N^2}$$
10. Average of the Signal RMS Envelope; RMS_mean  = \(\frac{1}{N} \sum_{n=1}^{N} RMS_n\)

And the following frequency-domain features:

1. Mean Signal Frequency; \(mF = \frac{\sum_{n=1}^{F} SP_n \cdot f_n}{\sum_{n=1}^{F} SP_n}\)
2. Average Waveform Length; \(W_L = \frac{1}{mF}
   \)

From section 2.3 and the previously mentioned features, we have a 4×12 feature array for each time window. This array has a fixed size regardless of the time window length and therefore helps the classifier to be indifferent to the joint motion speed. Thus, the input layer of the ANN classifier is set to be 48. One positive side effect of having multiple signal features is the compensation for a relatively low number of sEMG signal electrodes [35], as we examined only four muscles in this study.

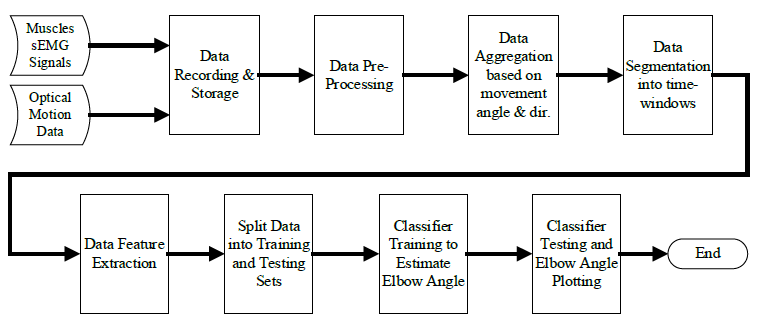
Since the angular range of motion of a healthy human’s elbow joint flexion-extension movement is [0°,145°] [36], we have selected the classes to be 0°, -5°, and +5° to keep the estimation resolution at 5° or 3.45% at a theoretical 100% classification accuracy. Where 0° represents a no-movement, -5° represents 5° flexion movement, and +5° represents 5° extension movement. However, 100% classification accuracy is hard to achieve especially with sEMG data, therefore, we have added two more classes -10°, and +10° to boost the overall classification accuracy. This is true because classes having the same direction but different displacements have more features similarity than classes with the same displacement and different direction. Therefore, the classifier is more likely to miss classify +5° as +10° than to miss classify +5° as -5° and vice versa. So, adding these extra two classes will aid in keeping the classification accuracy within 5°. As a result, the output layer of the ANN classifier is set to be 5, corresponding to 5 distinct classes. We have chosen Matlab R2020a to build the estimator and hence the classifier; Figure 2 shows a block diagram of the designed ANN classifier, Figure 3 shows the data flow throughout the elbow joint motion estimation system.

2.6. Estimation Results

This section shows the results of the elbow joint movement estimation. We first begin by training the ANN soft-max classifier for the training data set for a maximum of 4000 epochs. Training data and testing data of biceps curl motion confusion matrices are shown in Figure 4 and Figure 5 respectively.

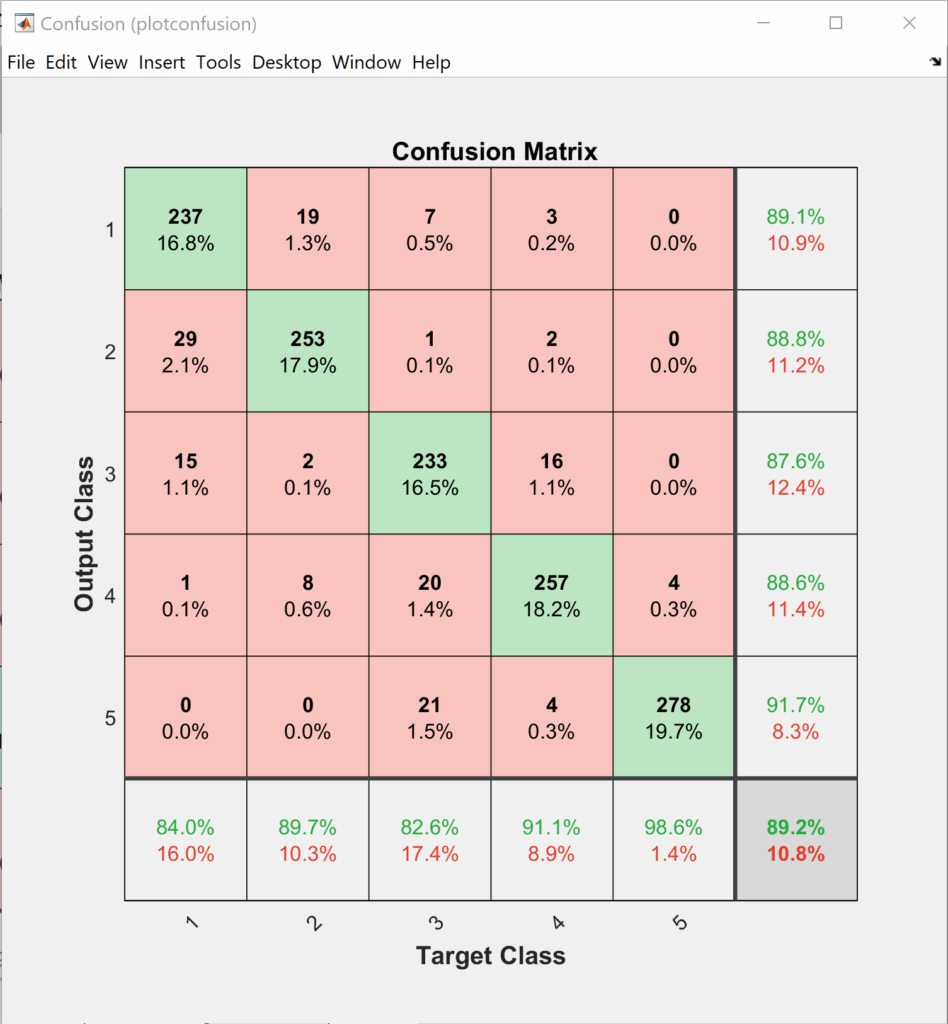
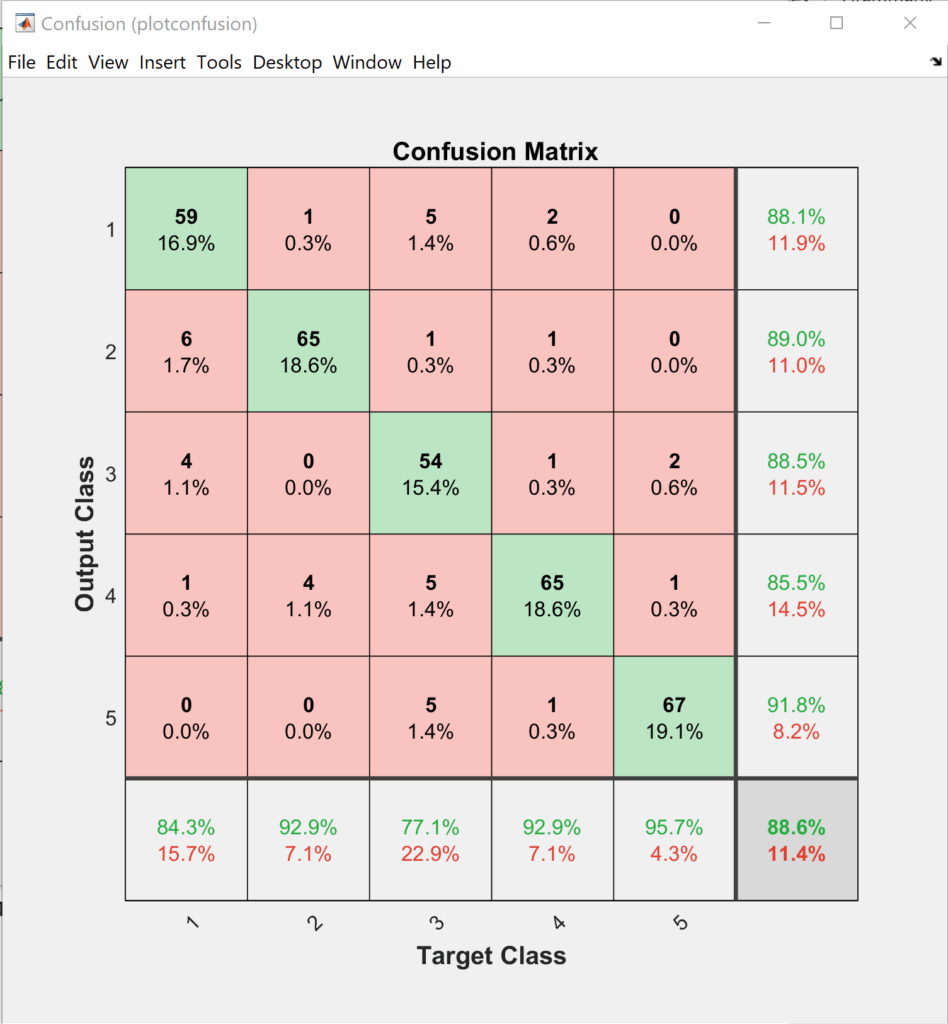
The order of the classes at the output layer of the classifier is as follows +5°, +10°, -5°, -10°, and 0°. If we look closer into Figure 4 and Figure 5 we can notice that most of the confusion happens between the same direction motions. So, if we do a simple probability analysis on the testing data, we can see that adding the two longer displacement classes helps in keeping the error within 5°.

$$k_{+5^\circ} = 88.1\%\ ;\ k_{+10^\circ} = 89\%\\ k_{-5^\circ} = 88.5\%\ ;\ k_{+10^\circ} = 85.5\% \\ k_{+5^\circ \text{ or } +10^\circ} = 88.1\% + 89\% – (88.1\% \times 89\%) = 98.69\% \\ k_{-5^\circ \text{ or } -10^\circ} = 88.5\% + 85.5\% – (88.5\% + 85.5\%) = 98.33\%$$

Adding two longer displacement classes helps in increasing the accuracy of the classifier in determining the direction to more than 98%. This is true because most of the confusion happens between the same direction movement as they have more similarity across their features.

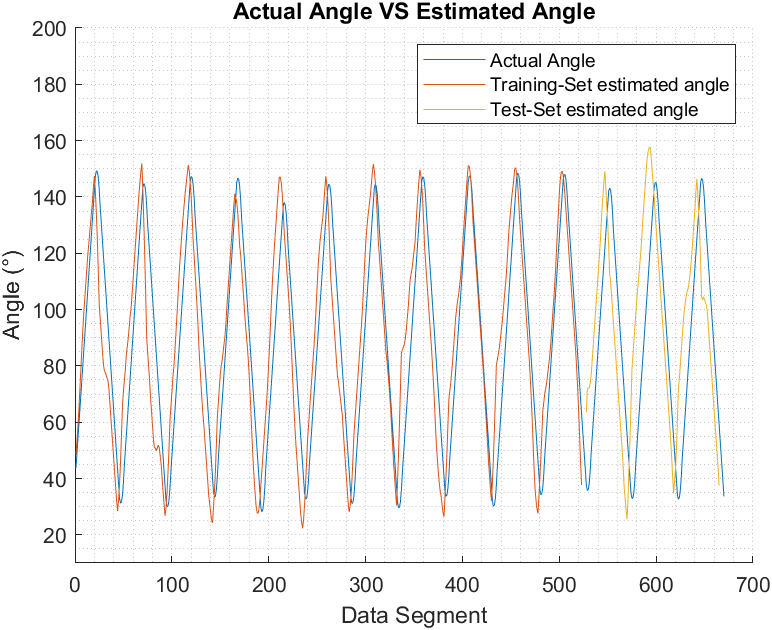
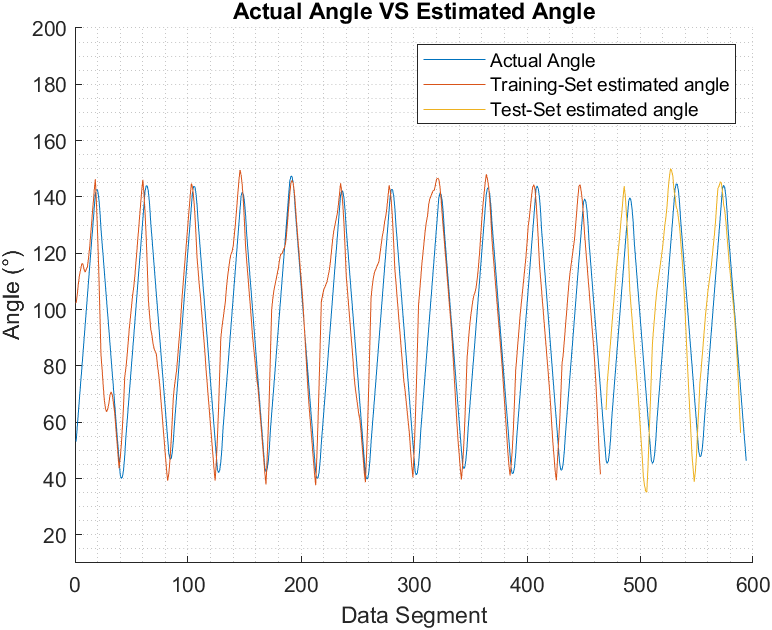
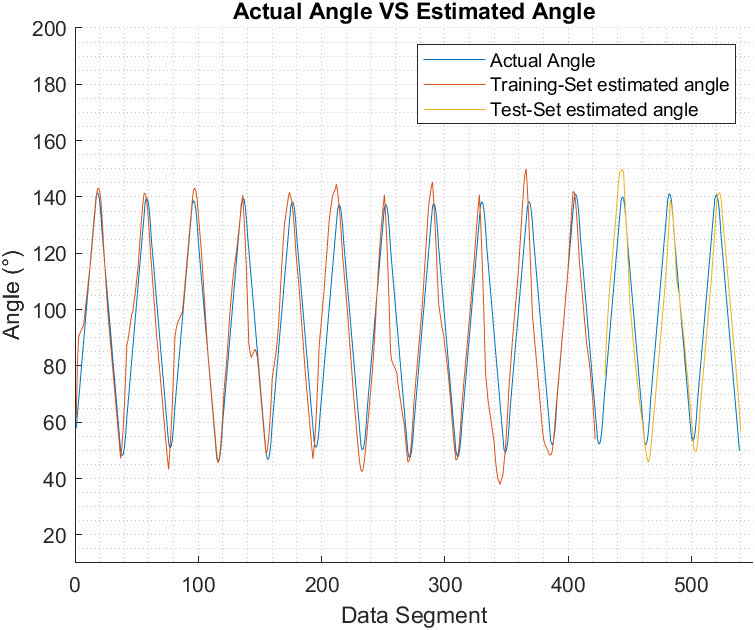
Figure 6, Figure 7, and Figure 8 show the actual joint angle versus estimated angle, training and testing data, for biceps curl with 5 pounds weight, biceps curl empty-handed and arm at shoulder level flexion and extension respectively.

We have chosen Pearson Correlation Coefficient (PCC) as a performance index when comparing the estimated elbow angle against the actual angle because unlike other commonly used performance indices, it is proven to be more accurate in representing the statistical association between two continuous variables as it employs the covariance between the two variables in its calculation [37]. PCC value ranges from +1 to -1, the closest it gets to +1 the more the two vectors are similar to each other. PCC can be found using (9) [16]:

$$PCC(Sig_1, Sig_2) = \frac{\mathrm{cov}(Sig_1, Sig_2)}{\sigma_{Sig_1} \cdot \sigma_{Sig_2}} \tag{9}$$

Where
cov(𝑆i_𝑔1 , 𝑆i_𝑔2) is the covariance of 𝑆i_𝑔1 and 𝑆i_𝑔2 which is given by (10)

$$\mathrm{cov}(A, B) = \frac{1}{N – 1} \sum_{i=1}^{N} (A_i – \mu_A)^* (B_i – \mu_B) \tag{10}$$

μ_x is the mean of 𝑥𝑥, which is given by \(\mu_x = \frac{1}{N} \sum_{n=1}^{N} x_{n’}\) and (∗) denotes the complex conjugate.

σ_𝑆i𝑔1 and σ_𝑆i𝑔2 are the standard deviation of 𝑆i_𝑔1 and 𝑆i_𝑔2 respectively and it’s given by (11)

$$S = \sqrt{ \frac{1}{N-1} \sum_{n=1}^{N} \left| A_n – \mu \right|^2 }\tag{11}$$

Table 1 list the PCC values for the estimated elbow joint movements for both training and testing sets for the designated movement.

Table 1: Elbow joint movement estimation correlation coefficient.

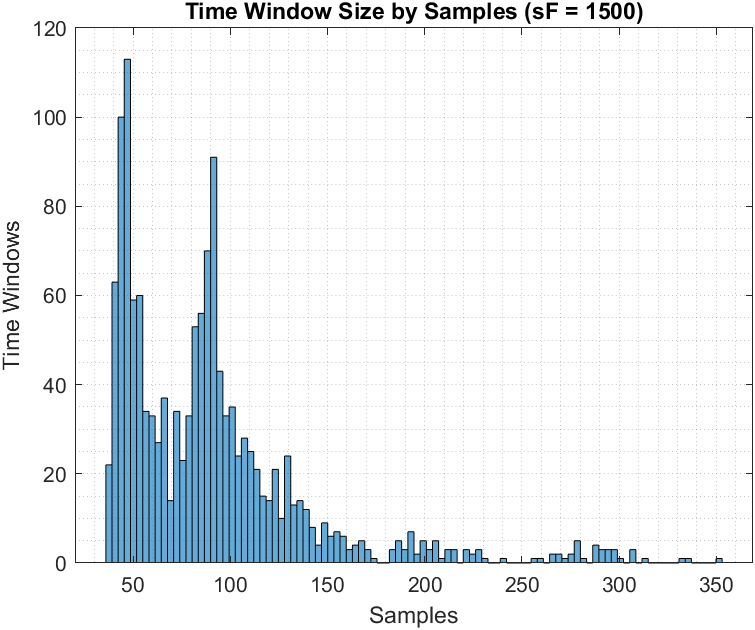
Figure 9 shows the histogram of time-window length in seconds for weighted biceps curls (i.e., 5 lbs) which in turn shows that the estimator was able to work with a variety of time-window sizes for the same angular displacement (and thus variable speeds) and still maintain high accuracy, i.e. +80% in classification and 0.91 in correlation.

3. Discussion

This work describes human’s upper limb movement estimation using sEMG data. We have designed an estimator that can estimate elbow joint movement immediately after the neural command sensed through sEMG signals at the muscles. Three muscles were targeted in this work, biceps brachialis, and triceps. The raw sEMG signal underwent preprocessing before it was fed to the estimator. The estimator used a combination of time and frequency domain features extracted for each sEMG channel. The features array is then fed to an ANN-based softmax classifier to be trained to classify five classes in joint angle displacement. The classifier had an accuracy ranging from 80- 90% for different effort levels and limb orientation. The classification was easier for the classifier when the participant carried weight in his hand, which increase the accuracy by 5-7%. The selection of the classes and the accuracy of the classifier translates to PCC between actual and estimated angles ranging from 0.91 to 0.95.

This study aimed to estimate the voluntary movement of upper extremities at the joint level. Since the appendicular skeleton has 126 bones [22], it’s not feasible to estimate all the joints movements in one study. To compensate for that we build an estimator that is modular from the software point of view. We believe the developed estimator can work to estimate the movement of any joint in the appendicular skeleton with no modification if we use 4 sEMG channels per joint per degree-of-freedom; assuming that we can properly distinguish agonistic and antagonistic muscles for the chosen joint.

We have chosen the elbow joint for this study because of three main reasons: first, ease of access to its agonistic and antagonistic muscle groups; second, its movement can be done in different planes with respect to the torso; and third, we can vary the joint load easily by asking the participant to hold weights. The last two reasons are essential to check the versatility of the estimator and to make sure it has consistent estimation in different movement conditions. We see this as a necessity because all the related literature reviewed in this study did not account for such variation during joint movement estimation  [11–16]. Furthermore, we validate the estimator across the whole dataset by implementing a five-fold cross-validation technique when training and testing the estimator.

Being based on ANN, the softmax classifier took a relatively long time to be trained, and it averaged about 30 minutes for the whole data set. But, on the other hand, the average estimation time per segment was about 1 microsecond, and according to the research in [38], this speed is more than sufficient for real-time applications. We used Windows 10 Pro 64-bit PC with Intel Core i7-4790K CPU and 32 GB RAM and Matlab R2020a to train and test the estimator, which can be a valid option for some but not all Human Machine Interface (HMI) applications targeted to benefit from this study.

The developed estimator can predict the current data segment joint angle with high accuracy regardless of the previous and the next data segment angle estimation accuracy.  In other words, misestimation in a single data segment doesn’t affect the consecutive data segments. Moreover, due to the selected movement classes, any misestimation will stay within the set 5° resolution which is reflected by the high PCC values shown in Table 1. The choice of features across time-domain and frequency-domain, the choice of classes, and the choice of the classifier all contributed to high estimation accuracy with 0.91 to 0.95 correlation between actual and estimated elbow angle by using only four sEMG sensors on the joint’s agonistic and antagonistic muscles.

4. Conclusion

The designed estimator achieved higher accuracy in joint movement estimation regardless of the joint orientation, speed, or effort level than the similar work reviewed in this paper. Which introduces the ability to continuously track the intended movement of the elbow joint with more than 90% correlation. Although the proposed estimator in this work doesn’t have 100% joint movement estimation accuracy, section 2.6 and Figures 5 to 8 show that the estimator has over 98% accuracy in predicting the direction of the movement even if it makes a mistake whether the movement is 5° or 10°, as its error margin to predict the wrong direction of movement is less than 2%.

And since the sEMG signals from able-bodied can be used to simulate the human limbs response in amputees [17,39,40], this work can be of great help towards a more natural myoelectric-prosthesis action, and it can also be used to other HMI applications.

1. Hefftner, W. Zucchini, G.G. Jaros, “The electromyogram (EMG) as a control signal for functional neuromuscular stimulation. I. Autoregressive modeling as a means of EMG signature discrimination,” IEEE Transactions on Biomedical Engineering, vol. 35, no. 4, pp. 230–237, 1988, doi:10.1109/10.1370.
2. Hefftner, G.G. Jaros, “The electromyogram (EMG) as a control signal for functional neuromuscular stimulation. II. Practical demonstration of the EMG signature discrimination system,” IEEE Transactions on Biomedical Engineering, vol. 35, no. 4, pp. 238–242, 1988, doi:10.1109/10.1371.
3. V. Basmajian, C.J. De Luca, Muscle Alives: Their Functions Revealed by Electromyographic, 5th ed, Williams & Wilkins, Baltimore, 1985.
4. Ju, G. Ouyang, H. Liu, “EMG-EMG correlation analysis for human hand movements,” Proceedings of the 2013 IEEE Workshop on Robotic Intelligence in Informationally Structured Space, RiiSS 2013 – 2013 IEEE Symposium Series on Computational Intelligence, SSCI 2013, no. Mi, pp. 38–42, 2013, doi:10.1109/RiiSS.2013.6607927.
5. C. Doerschuk, D.E. Gustafson, A.S. Willsky, “Upper Extremity Limb Function Discrimination Using EMG Signal Analysis,” IEEE Transactions on Biomedical Engineering, vol. BME-30, no. 1, pp. 18–29, 1983, doi:10.1109/TBME.1983.325162.
6. Asghari Oskoei, H. Hu, “Myoelectric control systems-A survey,” Biomedical Signal Processing and Control, vol. 2, no. 4, pp. 275–294, 2007, doi:10.1016/j.bspc.2007.07.009.
7. Dyson, K. Nazarpour, “Data Driven Spatial Filtering Can Enhance Abstract Myoelectric Control in Amputees,” 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), pp. 3770–3773, 2018.
8. A. Johnson, A.J. Fuglevand, “Mimicking muscle activity with electrical stimulation,” Journal of Neural Engineering, vol. 8, no. 1, pp. 1–25, 2011, doi:10.1088/1741-2560/8/1/016009.
9. H. Smith, L.J. Hargrove, “Comparison of surface and intramuscular EMG pattern recognition for simultaneous wrist/hand motion classification,” Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, pp. 4223–4226, 2013, doi:10.1109/EMBC.2013.6610477.
10. N. Kamavuako, J.C. Rosenvang, R. Horup, W. Jensen, D. Farina, K.B. Englehart, “Surface versus untargeted intramuscular EMG based classification of simultaneous and dynamically changing movements,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 21, no. 6, pp. 992–998, 2013, doi:10.1109/TNSRE.2013.2248750.
11. M. Aung, A. Al-Jumaily, “Estimation of upper limb joint angle using surface EMG signal,” International Journal of Advanced Robotic Systems, vol. 10, , pp. 1–8, 2013, doi:10.5772/56717.
12. Uchiyama, T. Bessho, K. Akazawa, “Static torque — angle relation of human elbow joint estimated with artificial neural network technique,” Journal of Biomechanics, vol. 31, , pp. 545–554, 1998.
13. Triwiyanto, O. Wahyunggoro, H.A. Nugroho, Herianto, “Evaluating the linear regression of Kalman filter model on elbow joint angle estimation using electromyography signal,” in AIP Conference Proceedings, 020004, 2018, doi:10.1063/1.5054408.
14. L. Li, Y. Song, Z.G. Hou, “Estimation of Lower Limb Periodic Motions from sEMG Using Least Squares Support Vector Regression,” Neural Processing Letters, vol. 41, no. 3, pp. 371–388, 2015, doi:10.1007/s11063-014-9391-4.
15. Xiao, Y. Wang, Y. Gao, Y. Zhu, J. Zhao, “Continuous estimation of joint angle from electromyography using multiple time-delayed features and random forests,” Biomedical Signal Processing and Control, vol. 39, no. December, pp. 303–311, 2018, doi:10.1016/j.bspc.2017.08.015.
16. Xiao, Y. Wang, Y. Gao, Y. Zhu, J. Zhao, “Continuous estimation of elbow joint angle by multiple features of surface electromyographic using grey features weighted support vector machine,” Journal of Medical Imaging and Health Informatics, vol. 7, no. 3, pp. 574–583, 2017, doi:10.1166/jmihi.2017.2054.
17. G. Ngeo, T. Tamei, T. Shibata, “Continuous and simultaneous estimation of finger kinematics using inputs from an EMG-to-muscle activation model,” Journal of NeuroEngineering and Rehabilitation, vol. 11, no. 1, pp. 1–14, 2014, doi:10.1186/1743-0003-11-122.
18. Wang, Y. Gao, J. Zhao, T. Yang, Y. Zhu, “Prediction of sEMG-based tremor joint angle using the RBF neural network,” 2012 IEEE International Conference on Mechatronics and Automation, ICMA 2012, pp. 2103–2108, 2012, doi:10.1109/ICMA.2012.6285668.
19. Van Der Riet, R. Stopforth, G. Bright, O. Diegel, “An overview and comparison of upper limb prosthetics,” 2013 Africon, vol. 9, no. 2, pp. 1–8, 2013, doi:10.1109/AFRCON.2013.6757590.
20. Nurhanim, I. Elamvazuthi, P. Vasant, S. Parasuraman, “Determination of Mathematical Model and Torque Estimation of s-EMG Signals based on Genetic Algorithm,” vol. 4, no. 5, pp. 135–139, 2013.
21. Shin, J. Kim, Y. Koike, “A Myokinetic Arm Model for Estimating Joint Torque and Stiffness From EMG Signals During Maintained Posture,” Journal of Neurophysiology, vol. 101, no. 1, pp. 387–401, 2009, doi:10.1152/jn.00584.2007.
22. L. Drake, A.W. Vogl, A.W.M. Mitchell, GRAY’S ANATOMY FOR STUDENTS, THIRD EDIT, CHURCHILL LIVINGSTONE ELSEVIER, Philadelphia, Pa, 2015.
23. Fornalski, R. Gupta, T.Q. Lee, “Anatomy and biomechanics of the elbow joint,” Techniques in Hand & Upper Extremity Surgery, vol. 7, no. 4, pp. 168–178, 2003, doi:10.1055/s-0033-1361587.
24. Gazzoni, N. Celadon, D. Mastrapasqua, M. Paleari, V. Margaria, P. Ariano, “Quantifying Forearm Muscle Activity during Wrist and Finger Movements by Means of Multi-Channel Electromyography,” PLoS ONE, vol. 9, no. 10, pp. e109943, 2014, doi:10.1371/journal.pone.0109943.
25. B.I. Reaz, M.S. Hussain, F. Mohd-Yasin, “Techniques of EMG signal analysis: Detection, processing, classification and applications,” Biological Procedures Online, vol. 8, no. 1, pp. 11–35, 2006, doi:10.1251/bpo115.
26. Zhang, P. Xu, P. Li, K. Duan, Y. Wen, Q. Yang, T. Zhang, “Noise ‑ assisted multivariate empirical mode decomposition for multichannel EMG signals,” Biomedical Engineering Online, vol. 16, no. 1, pp. 1–17, 2017, doi:10.1186/s12938-017-0397-9.
27. Haris, P. Chakraborty, B.V. Rao, “EMG signal based finger movement recognition for prosthetic hand control,” International Conference Communication, Control and Intelligent Systems, CCIS 2015, pp. 194–198, 2016, doi:10.1109/CCIntelS.2015.7437907.
28. H. Chowdhury, M.B.I. Reaz, M.A. Bin Mohd Ali, A.A.A. Bakar, K. Chellappan, T.G. Chang, “Surface electromyography signal processing and classification techniques,” Sensors (Switzerland), vol. 13, no. 9, pp. 12431–12466, 2013, doi:10.3390/s130912431.
29. Muceli, A.T. Boye, A. Avella, D. Farina, “Identifying Representative Synergy Matrices for Describing Muscular Activation Patterns During Multidirectional Reaching in the Horizontal Plane,” Journal of Neurophysiology, vol. 103, no. 3, pp. 1532–1542, 2010, doi:10.1152.
30. Nazmi, M. Abdul Rahman, S.-I. Yamamoto, S. Ahmad, H. Zamzuri, S. Mazlan, “A Review of Classification Techniques of EMG Signals during Isotonic and Isometric Contractions,” Sensors, vol. 16, no. 8, pp. 1304, 2016, doi:10.3390/s16081304.
31. A.K. Guanglin Li, Aimee E. Schultz, “Quantifying Pattern Recognition—Based Myoelectric Control of Multifunctional Transradial Prostheses,” IEEE TRANSACTIONS ON NEURAL SYSTEMS AND REHABILITATION ENGINEERING, vol. 18, no. 2, pp. 185–192, 2010, doi:10.1109/TNSRE.2009.2039619.
32. Scheme, K. Englehart, “Electromyogram pattern recognition for control of powered upper-limb prostheses: State of the art and challenges for clinical use,” Journal of Rehabilitation Research & Development, vol. 48, no. 6, pp. 643–660, 2011, doi:10.1682/JRRD.2010.09.0177.
33. Bishop, Pattern Recognition and Machine Learning, Springer, 2006.
34. R. Shewchuk, An Introduction to the Conjugate Gradient Method Without the Agonizing Pain, 1994.
35. Miljković, M.S. Isaković, “Effect of the sEMG electrode (re)placement and feature set size on the hand movement recognition,” Biomedical Signal Processing and Control, vol. 64, , pp. 102292, 2021, doi:10.1016/j.bspc.2020.102292.
36. D. Bryce, A.D. Armstrong, “Anatomy and Biomechanics of the Elbow,” Orthopedic Clinics of North America, vol. 39, no. 2, pp. 141–154, 2008, doi:10.1016/j.ocl.2007.12.001.
37. Benesty, J. Chen, Y. Huang, “On the importance of the pearson correlation coefficient in noise reduction,” IEEE Transactions on Audio, Speech and Language Processing, vol. 16, no. 4, pp. 757–765, 2008, doi:10.1109/TASL.2008.919072.
38. J. Young, L.J. Hargrove, T.A. Kuiken, S. Member, “The Effects of Electrode Size and Orientation on the Sensitivity of Myoelectric Pattern Recognition Systems to Electrode Shift,” IEEE Transactions on Biomedical Engineering, vol. 58, no. 9, pp. 2537–2544, 2011, doi:10.1109/TBME.2011.2159216.
39. Campbell, A. Phinyomark, A.H. Al-timemy, R.N. Khushaba, G. Petri, “Differences in EMG Feature Space between Able-Bodied and Amputee Subjects for Myoelectric Control,” 2019 9th International IEEE/EMBS Conference on Neural Engineering (NER), pp. 33–36, 2019.
40. V. Ravindra, C. Castellini, “A comparative analysis of three non-invasive human-machine interfaces for the disabled,” Frontiers in Neurorobotics, vol. 8, no. October, pp. 1–10, 2014, doi:10.3389/fnbot.2014.00024.

Citations by Dimensions

Citations by PlumX

Crossref Citations

1. Abdullah Y. Al-Maliki, Kamran Iqbal, Gannon White, “Fast Labeled Spanning Tree in Binary Irregular Graph Pyramids”, Journal of Engineering Research and Sciences, vol. 1, no. 10, pp. 69–78, 2022. doi: 10.55708/js0110009