An Optimized Algorithm for Solving the Maximum Independent Set Problem
Journal of Engineering Research and Sciences, Volume 4, Issue 8, Page # 24-30, 2025; DOI: 10.55708/js0408003
Keywords: Quantum-inspired genetic algorithm, Genetic algorithm, Maximum independent set problem, Search based software engineering, Software engineering
(This article belongs to the Section Quantum Science and Technology (QST))
Export Citations
Cite
Hussein, H. (2025). An Optimized Algorithm for Solving the Maximum Independent Set Problem. Journal of Engineering Research and Sciences, 4(8), 24–30. https://doi.org/10.55708/js0408003
Hager Hussein. "An Optimized Algorithm for Solving the Maximum Independent Set Problem." Journal of Engineering Research and Sciences 4, no. 8 (August 2025): 24–30. https://doi.org/10.55708/js0408003
H. Hussein, "An Optimized Algorithm for Solving the Maximum Independent Set Problem," Journal of Engineering Research and Sciences, vol. 4, no. 8, pp. 24–30, Aug. 2025, doi: 10.55708/js0408003.
Software engineering plays an important role in computer science. Novel quantum algorithms can efficiently solve software-engineering problems. Not only software engineering but also many industries including logistics, finance, genomics, resource allocation, logistics, bioinformatics, mobile agents and more have optimization problems. Such problems may have long time solutions. Research has been conducted to improve the performance of current solutions and to search for optimized solutions. Search-based software engineering (SBSE) uses computational techniques to determine optimized solutions in a large search space. There are SBSE problems such as Test Suite Minimization (TSM) and Maximum Independent Set (MIS) that require efficient solutions due to its important role. A quantum-inspired genetic algorithm had solved the TSM problem with higher performance than classical solutions. The quantum-inspired genetic algorithm and quantum algorithm showed better performance results than classical solutions. This improvement motivated us to modify such algorithms in order to solve the MIS optimization problems. In addition, MIS has crucial applications in many domains. It can be applied in software engineering to separate related and unrelated requirements, which is of great support for project management. Resources, time, cost, and relevance can be updated accordingly. MIS can also be applied in network design, scheduling, resource allocation, logistics, bioinformatics, mobile agents, and more. Quantum-inspired genetic algorithm combines quantum mechanics concepts and genetic algorithms which enhances search capability and provides efficient search mechanism. In this study, a modified quantum-inspired genetic algorithm (QIGA) is proposed and implemented to find an optimized solution for the MIS problem. A classical genetic algorithm (GA) is implemented and has been tested. A Comparison is conducted to show the results of QIGA and GA to measure the performance improvement. Results and its analysis are displayed to show QIGA and GA convergence. The proposed algorithm has no prior assumptions.
1. Introduction and Literature Review
Search-based software engineering (SBSE) uses computational techniques to determine optimized solutions for software engineering problems with a large and complex search space [1]. It combines software engineering concepts with optimization algorithms. It is difficult to solve complex software engineering issues manually; SBSE considers automation and optimization for solving such issues [2].
SBSE can be applied in many software engineering areas. Areas include, but are not limited to, software project management, software testing, software defect prediction, and automated program repair. Genetic Improvement (GI) is a field of SBSE that considers evolutionary computing in the automation of updating the software source code to best serve its non-functional requirements [2].
SBSE is used in enterprise application integration (EAIs). EAI is a research concern because of the growing need for data exchange and the reuse of functionality among applications. Thus, SBSE can be used in different phases of the software development lifecycle [3]. It can also be used in optimization techniques. It can be used to modify software to make it more efficient in terms of speed and resource use [4]. Examples of optimization problems that can be formulated as a search problem are the Test Suite Minimization problem and the Maximum Independent Set (MIS) problem [5].
The MIS problem is a nondeterministic polynomial (NP)-complete problem in which there is no known classical 1 1 algorithm that solves the problem efficiently [3]. An independent set is a set of vertices in a graph is the one in which no two vertices are adjacent. This means that if there is a set S of vertices, then for every two vertices in S there is no edge connecting them [6].
In [7], the author studied the maximum independent set with mobile myopic luminous robots on a grid network whose size is finite but unknown to the robots. It was performed under the assumption that robots are asynchronous, anonymous, silent, and they execute the same distributed algorithm.
In [8], the authors performed experimental adiabatic quantum computation (AQC) of the MIS problem on the Rydberg-atom system. They prepare an 11-by-18 array of optical tweezers. This lattice is identical to the Union-jack-like king graph experimented by [8], in which the NP completeness of the MIS problem has been addressed. On 198 optical tweezer traps, atoms are stochastically loaded at approximately 50%, and the resulting random graphs are used [5].
In [9], the researchers proposed an optimized solution for the k-independent set problem for a graph. It proved mathematically that since the number of vertices in the independent set of each finite graph is finite, then the number of vertices in the k-independent set k has a maximum. It explained the mathematical proof with neither implementation nor performance measurement.
In [10], the authors applied automatic generation of algorithms to combine basic heuristics for the MIS problem. Then the space of generated algorithms is traversed by employing genetic programming. An algorithm is then selected depending on the computational performance of each generated algorithm.
In [11], the authors studied the maximum-independent-set problem on unit-disk graphs. They carried out numerical studies and assess problem hardness, using both exact and heuristic algorithms. They also showed that by relaxing the constraints on the classical simulated annealing algorithms considered in [8], their implementation became competitive with quantum algorithms.
In [8], the authors used Rydberg atom arrays with up to 289 qubits in two spatial dimensions to solve the maximum-independent-set problem. Quantum algorithms for optimization were implemented via global atomic excitation using homogeneous laser pulses with a time-varying Rabi frequency Ω(t)eiø(t) and detuning Δ(t). It was concluded that grover-type algorithms have a quadratic speedup greater than the brute-force classical search. It was also observed that in the hardest graphs, superlinear quantum speedup exists in finding exact solutions in the deep-circuit regime and analyzing its origins. In [8], the authors investigated whether instances with large Hamming distances between the local and global optima of independent set sizes |MIS – 1| and |MIS| are related to the overlap gap property of the solution space.
In [6], the authors published an algorithm for determining the maximum independent set problem using a combination of previous algorithms to solve the same problem. In this study, the minimum degree algorithm (MD) was conducted to solve the MIS problem. The MD reached results close to the target results, but failed to obtain the exact numbers in almost every graph. The density of the graph affected the results, as it worsened when the graph was in a higher density degree or it had a higher average degree per node. This study also implemented the controlled-MD approach, which achieved a better efficiency than MD. The controlled-MD efficiency is not affected by the graph density, but its results are close to the target and not exactly the same. To calculate the independent set size, the algorithm counts the number of vertices the independent set contains, while the maximum independent set is one of the largest possible sizes for a given graph.
The aim of this study is to find an optimized solution for the MIS problem. It proposes a modified genetic-inspired genetic algorithm that considers local and global parameters to improve the results. Crossover, mutation, interference, and quantum measurements are used to accelerate the convergence of the results. The fitness function calculated better results than classical GA. Results analysis is conducted to illustrate the algorithm contribution.
The remainder of this paper is organized as follows. Section 2 introduces the maximum independent set problem and the quantum-inspired genetic algorithm, along with its operations. In Section 3, the proposed algorithm is described. This illustrates the steps and operation details. It also displays various operators and how they work. In Section 4, the proposed algorithm is evaluated and its experimental results are presented. A comparison between the results of the proposed algorithm and the results of the classical GA solving the MIS problem is also shown in this section. Finally, Section 5 concludes the paper.
2. Background
2.1. Maximum Independent Set (MIS) Problem
The MIS is an SBSE problem in software engineering and it is an optimization problem in computer science and graph theory [12]. Given a connected, undirected graph G = (V, E) as the input, where V is the list of vertices and E is the list of edges. The algorithm attempts to find the largest subset S of V, such that no two vertices in S have an edge connecting them.
For example, Figure 1 shows a given maximum independent set problem for graph G with six vertices. Table 1 illustrates the representation of Figure 1 in matrix form with the vertices listed in the columns and repeated in the rows as V1, V2, V3, V4, V5, and V6, where (V1 and V2) represent the link between V1 and V2. If the cell value is 1, there is an edge connecting the two vertices that intersect in that cell. If the cell value is zero, then there is no edge between the two vertices intersecting in that cell. The solution is the vertex set {V2, V3, V5, V6}, which is not difficult to find but becomes more complicated with large datasets [13].
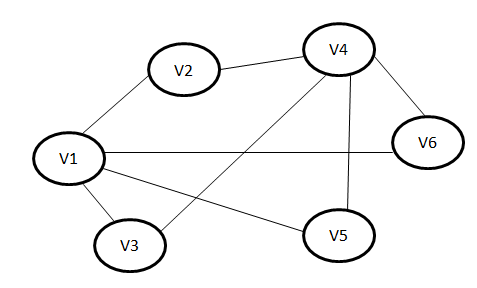
Table 1: Example for maximum independent set problem
Vertices | V1 | V2 | V3 | V4 | V5 | V6 |
V1 | 0 | 1 | 1 | 0 | 1 | 1 |
V2 | 1 | 0 | 0 | 1 | 0 | 0 |
V3 | 1 | 0 | 0 | 1 | 0 | 0 |
V4 | 0 | 1 | 1 | 0 | 1 | 1 |
V5 | 1 | 0 | 0 | 1 | 0 | 0 |
V6 | 1 | 0 | 0 | 1 | 0 | 0 |
2.2. Quantum Inspired Genetic Algorithm (QIGA)
2.2.1. Quantum Basics
Classical computers perform n operations simultaneously using n bits, while quantum computers perform 2n operations in n qubits simultaneously [14]. This relationship is exponential. Qubits can be in the superposition of |0> and |1>, such that α|0> + β|1>, where α and β are complex numbers with
$$|\alpha 2\rangle + |\beta 2\rangle = 1 \tag{1}$$
Here are some unitary logic gates’ effects (Hadmard gate [15]).
$$H.|0\rangle = \tfrac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}\begin{bmatrix} 1 \\ 0 \end{bmatrix} = \tfrac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ 1 \end{bmatrix} \tag{2}$$
$$H.|1\rangle = \tfrac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}\begin{bmatrix} 0 \\ 1 \end{bmatrix} = \tfrac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ -1 \end{bmatrix} \tag{3}$$
The X-gate, which is the NOT gate in classical computers, can have the following effect [15]:
$$X.|0\rangle = \tfrac{1}{\sqrt{2}}\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\begin{bmatrix} 1 \\ 0 \end{bmatrix} = \tfrac{1}{\sqrt{2}}\begin{bmatrix} 0 \\ 1 \end{bmatrix} = |1\rangle \tag{4}$$
$$X.|1\rangle = \tfrac{1}{\sqrt{2}}\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\begin{bmatrix} 0 \\ 1 \end{bmatrix} = \tfrac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ 0 \end{bmatrix} = |0\rangle \tag{5}$$
Basic quantum logic gates are used form quantum circuits.
2.2.2. QIGA Operations
The Quantum-Inspired Genetic Algorithm (QIGA) builds its operations in a qubit concept representation [16].
2.2.3. Quantum Mutation
It defines a mutation rate to randomly pick a mutation point and change the chromosome value by replacing that randomly picked point with another randomly chosen point. This is performed as follows [17]:
$$P = \begin{bmatrix} \alpha 1 & \alpha 2 & \alpha 3 & \ldots & \alpha q \\ \beta 1 & \beta 2 & \beta 3 & \ldots & \beta q \end{bmatrix} .\tag{6}$$
The new chromosome will become:
$$P’ = \begin{bmatrix} \alpha’ 1 & \alpha 2 & \alpha 3 & \ldots & \alpha q \\ \beta’ 1 & \beta 2 & \beta 3 & \ldots & \beta q \end{bmatrix} ,\tag{7}$$
where
$$|\alpha’ 2 \rangle + |\beta’ 2 \rangle = 1 .\tag{8}$$
2.2.4. Quantum Crossover
A crossover point is chosen randomly in two different chromosomes according to the crossover rate, and the operation is applied as follows [18]:
$$P1 = \begin{bmatrix} \alpha 1 & \alpha 2 & \alpha 3 & \ldots & \alpha q \\ \beta 1 & \beta 2 & \beta 3 & \ldots & \beta q \end{bmatrix} ,\tag{9}$$
$$P2 = \begin{bmatrix} \alpha’ 1 & \alpha’ 2 & \alpha’ 3 & \ldots & \alpha’ q \\ \beta’ 1 & \beta’ 2 & \beta’ 3 & \ldots & \beta’ q \end{bmatrix} .\tag{10}$$
After applying the crossover, the chromosomes will be as the following:
$$P’1 = \begin{bmatrix} \alpha 1 & \alpha’ 2 & \alpha’ 3 & \ldots & \alpha’ q \\ \beta 1 & \beta’ 2 & \beta’ 3 & \ldots & \beta’ q \end{bmatrix} ,\tag{11}$$
$$P’2 = \begin{bmatrix} \alpha’ 1 & \alpha 2 & \alpha 3 & \ldots & \alpha q \\ \beta’ 1 & \beta 2 & \beta 3 & \ldots & \beta q \end{bmatrix} .\tag{12}$$
2.2.5. Interference
The interference or rotation operator can be applied as follows [19]:
$$U(\Theta)|\psi_t\rangle = |\psi_{t+1}\rangle = \begin{bmatrix} \cos(\Theta)\alpha t – \sin(\Theta)\beta t \\ \sin(\Theta)\alpha t + \cos(\Theta)\beta t \end{bmatrix} .\tag{13}$$
3. The Proposed Technique
3.1. Problem Representation
The graph of the MIS problem is composed of nodes, and the edges between the nodes link these nodes. If there is no edge, the two nodes are not connected. This problem is represented in the proposed technique as a table with a list of nodes shown in rows and the same nodes shown in columns. The intersection between the node in the column and the node in the row shows whether there is an edge connecting them or not. The 0 value is for the no existing edge between the nodes while the 1 value is for the existing edge connecting the nodes. For example, if there is a link between two nodes V1 and V2, then the intersection of column V1 and row V2 takes a value of “1” and similarly the intersection of row V1 and column V2. “0” is put otherwise. An example is presented in Table 1. This table is then represented in a 2D matrix form. Table 1 can be represented as follows.
$$\text{MIS matrix} = \begin{bmatrix} 0 & 1 & 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 \end{bmatrix} \tag{14}$$
As shown in Figure 2 and Algorithm 1, the algorithm first generates or reads the MIS matrix. For each node a global α a global β are calculated as using (15) and (16). These global α and global β are not updated later on. Each matrix has various tests that use the global α and β. After selecting the chromosomes from the MIS matrix, local α and local β are calculated for each chromosome in the population. Local α and β are calculated using the global α and β. They are updated from one generation to another. Table 2 shows an example of the global α and global β for each row as calculated using (15) and (16). Table 3 gives an example of the local α and β for each chromosome in population “p” assuming a population size of 3.
Table 2: Global α and global β example.
Row Number | Global Values |
V1 | α1, β1 |
V2 | α2, β2 |
V3 | α3, β3 |
V4 | α4, β4 |
V5 | α5, β5 |
V6 | α6, β6 |
Table 3: Local α and local β example.
Chromosome Number | Chromosome(population, chromosome, row) | ||
1 | V1 αp11, βp11 | V3 αp13, βp13 | V5 αp15, βp15 |
2 | V2 αp22, βp22 | V4 αp24, βp24 | V5 αp25, βp25 |
3 | V3 αp33, βp33 | V5 αp35, βp35 | V6 αp36, βp36 |
$$\text{global\_}\beta = \sqrt{1.0 – \text{global\_}\beta^2} \tag{15}$$
$$\text{global\_}\alpha = \sqrt{\text{sumOfZeros}/\text{sumOfAllZeros}} \tag{16}$$
The matrix values are then considered individually in each row to calculate sumOfZeros and sumOfAllZeros. sumOfZeros is calculated when the intersection is zero and the adjacent node is zero, as shown in (17). If the intersection is zero, then sumOfAllZeros is calculated, as shown in (18). The fitness value can then be calculated, as illustrated in (19).
$$\text{sumOfZeros} = \sum_{k=0}^{colSize} \big((colSize – k)(k+1)\big) \tag{17}$$
$$\text{sumOfAllZeros} = \sum_{k=0}^{colSize} (colSize – k) \tag{18}$$
$$\text{fitnessValue} = \text{sumOfZeros}/\text{sumOfAllZeros} * 100 \tag{19}$$
4. Experimental Results
All the experiments are conducted in a laptop with Intel® Core™ i7 processor and 64-bit Windows 11 operating system.
A summary of the proposed technique is presented in the pseudocode of Algorithm 1. Figure 2 shows a flowchart for the proposed technique for visual clarity. The pseudocode and flowchart illustrates the QIGA process as it starts with the MIS matrix itself, then it generates the initial population and initializes the parameters including the local α and local β. Then a loop starts with applying interference operation. The fitness function is measured after the interference operation. Based on this measurement, parameters are updated and a population is selected. Crossover operation is applied on the selected population and then mutation operation is performed. The fitness function and the average fitness are then calculated. Then it updates the loop counter to go for the next iteration. These steps are performed as long as the predetermined number of iterations is not yet reached or the average fitness is less than 100. When this stopping condition becomes false, that means the MIS is solved and the algorithm ends. Table 4 lists the Genetic Algorithm (GA) parameters used to measure the technique. The experiments were performed on 200 × 200 matrices to represent a graph of 200 nodes. The experimental results were applied to three different types of matrices. The sparse that contains 80% of zeros and 20% of ones, the dense that contains 80% of ones and 20% of zeros, and the 50-50 that contains 50% of zeros and 50% of ones. The matrices are formed with randomly chosen values, but they follow each matrix type constraint.
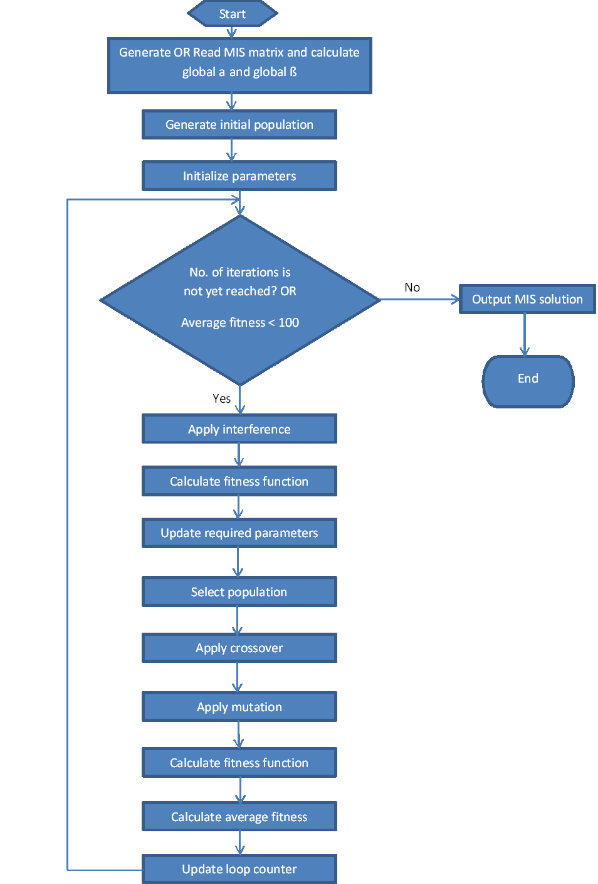
Algorithm 1: Pseudocode for the proposed technique |
Read MIS matrix m × n. Calculate global α and global β for each node. Calculate sumOfZeros and sumOfAllZeros as shown in (17) and (18). Choose a population size. Generate the initial population. Give initial values to the local α and local β. While number of iterations is not yet reached OR average fitness == 100 do Apply interference and measure the fitness results using the fitness function in (19). Update the local α and local β accordingly. Select from the population using Roulette wheel. Apply crossover with 90% . Apply mutation with a mutation rate 1% Measure the fitness results. Calculate the average fitness. Update loop counter. end while Print the MIS solution. |
The maximum independent set problem was solved using GA and QIGA. Both the algorithms were tested using the same parameters. A total of 500 iterations were performed ten times to measure the average of the results.
Table 4: GA Parameters for the proposed technique
GA Parameter | Value |
Population Size | 500 |
Crossover | Single-point |
Crossover Rate | %90 |
Mutation Rate | %1 |
Selection | Roulette Wheel |
ϴinitial | π |
δϴs | A random number between 0 and 1 |
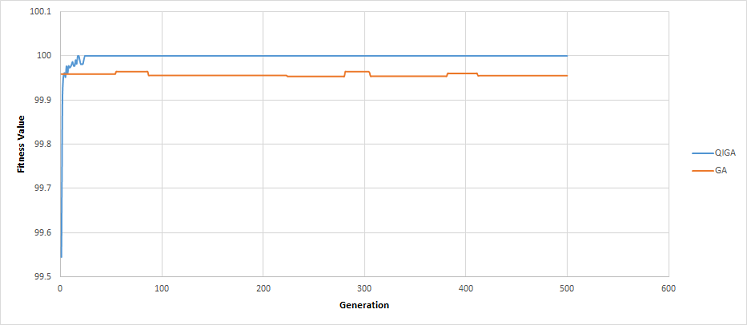
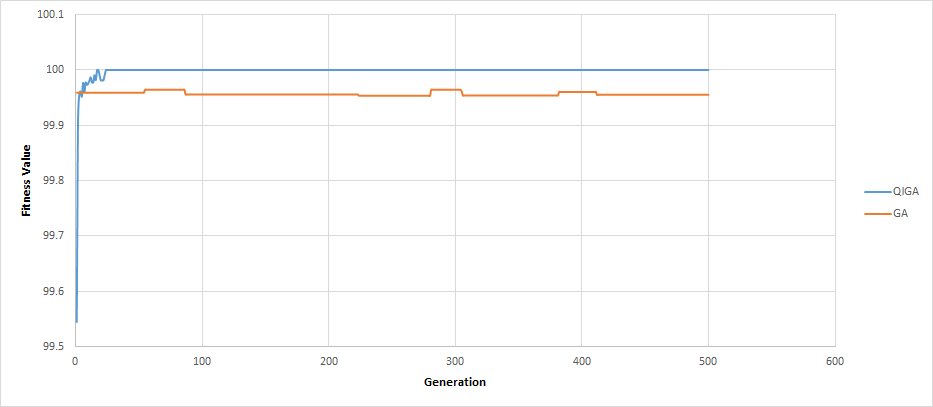
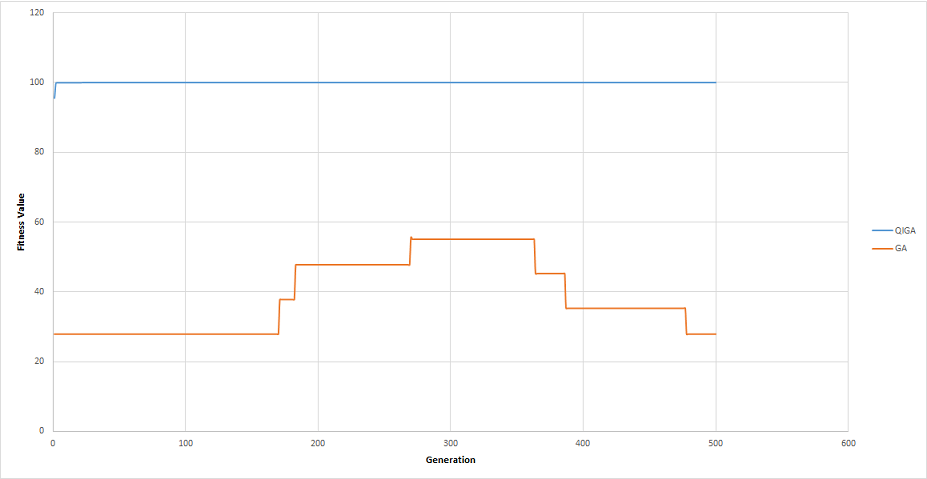
Figure 3, 4, and 5 show that QIGA achieved faster convergence than classical GA in the three matrix types. In addition to convergence, the QIGA fitness value results were higher than the classical GA results. Figure 3 shows the faster convergence and higher fitness values of sparse matrices, whereas Figure 4 shows the same successful results for balanced matrices. Figure 5 illustrates the convergence and results achieved for dense matrices.
5. Conclusion and Future Work
In this paper, a modified quantum-inspired genetic algorithm (QIGA) is proposed to solve the maximum independent problem, where quantum superposition has been used in the encoding of the chromosome to increase the size of the search space over approximately the same physical space. Quantum gates, such as crossover, mutation, and interference gates, have been used to achieve better and faster results. The experimental results have been shown for sparse, balanced, and dense test cases. The results show that QIGA performed faster and better than classical GA. It converges more rapidly and it achieved higher fitness values. This solution can be used in many domains such as software engineering to separate related requirements from unrelated requirements, time management, cost management, resource management, network design, scheduling, resource allocation, logistics, bioinformatics, mobile agents, and more [20]. Future work will be held on creating more fitness functions to give better results. Other problems will be considered to be solved using QIGA. Future application to the proposed technique can be performed on other domains.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The author received no direct funding for this research.
Funding
No financial support for this research.
Availability of data and materials
Data was generated and available upon request.
- Harman, Y. Jia, J. Krinke, W. B. Langdon, J. Petke, and Y. Zhang, “Search based software engineering for software product line engineering,” Sep. 2014, doi: 10.1145/2648511.2648513.
- Federica Sarro, “Search-Based Software Engineering in the Era of Modern Software Systems,” IEEE 31st International Requirements Engineering Conference (RE), 2023.
- Angela Mazzonetto, Rafael Z. Frantz, Fabricia Roos-Frantz, Carlos Molina-Jimenez, and Sandro Sawicki, “A Systematic Mapping Study of Search-Based Software Engineering for Enterprise Application Integration,” International Journal of Software Engineering and Knowledge Engineering, 2022.
- Memeti, S. Pllana, A. Binotto, J. Kołodziej, and I. Brandic, “Using meta-heuristics and machine learning for software optimization of parallel computing systems: a systematic literature review,” Computing, vol. 101, no. 8, pp. 893–936, Apr. 2018, doi: 10.1007/s00607-018-0614-9.
- Kim, M. Kim, J. Park, A. Byun, and J. Ahn, “Quantum computing dataset of maximum independent set problem on king lattice of over hundred Rydberg atoms,” Scientific Data, vol. 11, no. 1, Jan. 2024, doi: 10.1038/s41597-024-02926-9.
- Abdul Wahab Chaudhry, “A New Algorithm for Solving the Maximum Independent Set Problem,” Australia, May 2019.
- Kamei and S. Tixeuil, “An Asynchronous Maximum Independent Set Algorithm By Myopic Luminous Robots On Grids,” The Computer Journal, vol. 67, no. 1, pp. 57–77, Nov. 2024, doi: 10.1093/comjnl/bxac158
- Pichler, S. Wang, L. Zhou, S. Choi, and M. D. Lukin, “Quantum optimization of maximum independent set using Rydberg atom arrays,” Science, vol. 376, no. 6598, pp. 1209–1215, Jun. 2022, doi: 10.1126/science.abo6587.
- Luo and S. Ding, “Solving the k-Independent Sets Problem of Graphs by Gröbner Bases,” Open Journal of Discrete Mathematics, vol. 13, no. 03, pp. 86–94, 2023, doi: 10.4236/ojdm.2023.133008.
- Moisés Silva-Muñoz, C. Contreras-Bolton, C. Rey, and V. Parada, “Automatic generation of a hybrid algorithm for the maximum independent set problem using genetic programming,” Applied Soft Computing, vol. 144, pp. 110474–110474, Jun. 2023, doi: 1016/j.asoc.2023.110474.
- S. Andrist et al., “Hardness of the maximum-independent-set problem on unit-disk graphs and prospects for quantum speedups,” Physical review research, vol. 5, no. 4, Dec. 2023, doi: 10.1103/physrevresearch.5.043277.
- Dong, A. Goldberg, A. Noe, N. Parotsidis, M. Resende, and Q. Spaen, A Local Search Algorithm for Large Maximum Weight Independent Set Problems, 30th Annual European Symposium on Algorithms (ESA 2022), 2022.
- Wang, J. Tan, L. Zhu, and W. Huang, “Solving the Maximum Independent Set Problem based on Molecule Parallel Supercomputing,” Applied Mathematics & Information Sciences, vol. 8, no. 5, pp. 2361–2366, Sep. 2014, doi: 10.12785/amis/080531.
- Hakemi, M. Houshmand, S. A. Hosseini, and X. Zhou, “A Modified Quantum-Inspired Genetic Algorithm Using Lengthening Chromosome Size and an Adaptive Look-Up Table to Avoid Local Optima,” Axioms, vol. 12, no. 10, p. 978, Oct. 2023, doi: 10.3390/axioms12100978.
- S. Menon and M. Ritwik, “A Comprehensive but not Complicated Survey on Quantum Computing,” IERI Procedia, vol. 10, pp. 144–152, 2014, doi: 10.1016/j.ieri.2014.09.069.
- M. Mohammed, N. A. Elhefnawy, M. M. El-Sherbiny, and M. M. Hadhoud, “Quantum crossover-based quantum genetic algorithm for solving non-linear programming,” International Conference on Informatics and Systems, May 2012.
- Toronto and D. Ventura, “Learning Quantum Operators From Quantum State Pairs,” IEEE International Conference on Evolutionary Computation, vol. 3103, pp. 2607–2612, Sep. 2006, doi: 10.1109/cec.2006.1688634.
- Ridha, “Reversible Logic Synthesis Methodologies with Application to Quantum Computing,” Springer International Publishing, 2015. doi: 0.1007/978-3-319-23479-3.
- Hussein, A. Younes, and W. Abdelmoez, “Quantum-Inspired Genetic Algorithm for Solving the Test Suite Minimization Problem,” WSEAS TRANSACTIONS ON COMPUTERS, vol. 19, pp. 143–155, Aug. 2020, doi: 10.37394/23205.2020.19.20.
- M. Salman and A. S. Al-Jilawi, “Applications of maximum independent set,” AIP conference proceedings, Jan. 2022, doi: 10.1063/5.0093375.
- Hager Hussein, “Energy-Optimized Smart Transformers for Renewable-Rich Grids”, Journal of Engineering Research and Sciences, vol. 4, no. 10, pp. 21–28, 2025. doi: 10.55708/js0410003
- Hager Hussein, “Evolutionary Learning of Fuzzy Rules and Application to Forecasting Environmental Impact on Plant Growth”, Journal of Engineering Research and Sciences, vol. 1, no. 4, pp. 48–53, 2022. doi: 10.55708/js0104006
- Hager Hussein, “Distributed Approach for the Indoor Deployment of Wireless Connected Objects by the Hybridization of the Voronoi Diagram and the Genetic Algorithm”, Journal of Engineering Research and Sciences, vol. 1, no. 2, pp. 10–23, 2022. doi: 10.55708/js0102002

