The accelerating and unrestrained use of energy globally raises serious concerns for the future of the planet, primarily due to the environmental devastation caused by fossil fuels. Achieving high energy efficiency in both fuel-driven and renewable energy systems is crucial for future energy optimization. Clean energy production is one of the most effective strategies to mitigate climate change effects. These challenges necessitate a significant shift towards sustainable energy models, specifically smart and renewable energy systems that do not emit greenhouse gases during generation. This paper proposes a novel framework for smart and renewable energy optimization through the design of smart transformers that maximize energy savings without generating harmful radiation. The optimization utilizes a hybrid approach combining Nonlinear Programming (NLP) and an Artificial Intelligence (AI) technique, the Genetic Algorithm (GA), applied to specific transformer design parameters. The validated results demonstrate significant efficiency gains and cost reduction, strengthening the paper's contribution to robust, sustainable energy infrastructure.

1. Introduction  

This paper examines energy efficiency and renewable energy optimization as cornerstones for a sustainable future. In [1] and [2], the authors emphasize that as environmental degradation intensifies, marked by climate change, extreme weather, and biodiversity loss, the global community is aggressively driven to adopt clean energy solutions. These challenges demand a fundamental rethinking of energy models, requiring coordinated action across public administration, industry, and consumers by [3].

Recent projections indicate that global energy consumption will surge in the coming decades, primarily driven by rapid industrial expansion in emerging economies described by [3]. In response, renewable energy sources, including wind, solar, and hydro, are poised to play a central role. In [4] and [5], the authors highlighted that integrating these renewables not only enhances energy security but also directly addresses the forecasted doubling of energy demand by 2050. Consequently, optimizing energy conversion and minimizing waste—particularly within critical grid components—have emerged as critical priorities by [6].

A reduction in greenhouse gas emissions is directly achieved by accelerating the development and integration of renewable energy technologies, whose long-term objective is to supplant carbon-intensive energy dominating global markets by [7]. The central challenge lies in orchestrating an energy transition that efficiently manages consumption while promoting the extensive deployment of renewable sources. This is particularly relevant as innovative strategies incorporating Artificial Intelligence (AI), Machine Learning (ML), and advanced optimization methods are increasingly leveraged for complex grid management, power forecasting, and enhancing the resilience of components to fluctuating renewable loads by [6], [8] and [9].

Fossil fuels, the traditional backbone of large-scale energy production, are marked by finite reserves and geopolitical volatility. In contrast, renewable energy systems offer a sustainable alternative. The optimization of system components like power transformers can significantly bolster energy security and environmental resilience, as described in [10] and [11]. The economic viability and success of deploying these sustainable energy systems often relies on comprehensive planning, analysis, and optimization studies, as highlighted in the work by [12] and [13].

This paper introduces a novel methodology aimed at enhancing the integration of renewable energy through the energy optimization of smart distribution transformers. Specifically, the proposed framework employs a Nonlinear Programming (NLP) and Genetic Algorithm (GA) hybrid optimization technique to dynamically increase transformer efficiency and reduce losses without compromising operational integrity. By introducing a time-varying parameter model to accurately capture transformer non-linearity and estimating model parameters using this hybrid approach, the work builds on recent advances in optimization methods, as detailed in [5] and [14]. The need to account for core-specific factors, such as inter-laminar contacts and losses in magnetic cores, underscores the importance of the detailed modelling presented here, as discussed in [15]. Validation through simulated and experimental performance curves demonstrates the potential of these techniques to revolutionize transformer design and, by extension, promote a more robust, sustainable energy infrastructure for renewable-rich grids.

2. Proposed Design Methodology

2.1. Nonlinear Program (NLP) Optimization Technique

In transformer design optimization, NLP techniques are effective because design variables (e.g., number of turns, winding wire diameter, stacking factor, flux density, yoke height, window height, core leg width) can assume continuous and integer values, and the objective function and constraints are typically non-linear. The design vector  includes these physical parameters.

The general NLP problem seeks to find the design vector 𝒙 = (𝑥₁, 𝑥₂,……, 𝑥_𝑛) that minimizes the objective function 𝑓 (x), which represents the Total Cost of Ownership (TCO):

$$f(x) = \text{Cost}_{\text{Material}} + k \cdot \left(\text{Cost}_{\text{No-Load Losses}} + \text{Cost}_{\text{Load Losses}}\right) \tag{1}$$

Subject to constraints :  ցi(𝑥):𝑓or 𝑖=1,2,…,𝑚:

$$g_i(x) = \begin{cases} \leq 0 \\ = 0 \\ \geq 0 \end{cases}, \quad \text{with } x_l \leq x_i \leq x_u \text{ for all } i. \tag{2}$$

where 𝑥₁ and 𝑥_𝑢 are the lower and upper limits of the design variables, respectively by [15].

This work uses the exterior penalty function method, where the augmented function is formulated as:

$$P(x,r)=f(x)+r\sum_{i=0}^{m}\left[g_i(x)\right]^q,\quad r\ge 0,\ q\ge 1$$

where 𝑔_𝑖(x) is defined as max [ 𝑔_𝑖(x), 0] and q is typically 2. The minimization process continues, and as the penalty multiplier 𝑟 → ∞, the minimization of the penalty function converges to the constrained minimization of the objective function:

$$\min P(x,r)\rightarrow \min f(x)\tag{3}$$

2.2. Genetic Algorithm (GA) Optimization Technique

Genetic Algorithms (GAs) are stochastic methods based on evolutionary principles: competition for survival and reproduction of the fittest individuals by [15]. In this hybrid approach, the NLP solution is validated and refined using the GA. NLP determines core design parameters, while GA is specifically used here for estimating time-varying parameters (e.g., core model parameters) and validating overall performance through objective function minimization. This synergistic approach enhances exploration at the start (GA) and exploitation for final fine-tuning (NLP) by [6].

2.3. Electrical Equivalent Optimization Technique

Accurate modelling of the power transformer core’s non-linearity and magnetic losses is essential for high efficiency. This study models the transformer using equivalent electrical circuits where windings 1 and 2 have N₁ and N₂ turns, respectively. The non-linear behaviour is accounted for by considering the magnetic flux distribution, which necessitates introducing the concept of equivalent flows and time-varying circuit parameters.

The electrical resistance of the windings was determined using the highly accurate Kelvin Bridge method. No-load losses (core losses) were obtained using a distorted waveform supply and then referred to the pure sinusoidal voltage by an equation considering the supply voltage’s form factor. The short-circuit impedance, calculated from the load loss test data, was used to determine voltage regulation.

3. Formulation of the Design Problem

The Genetic Algorithm was applied as an estimation method to find a solution to the complex non-linear system by estimating a parameter vector 𝑋_𝐴G, which includes variables crucial for modelling the equivalent circuit:

$$X_{AG} = [R_1, X_1, R_2, X_2, R_m, X_m] \tag{4}$$

The GA objective function 𝐹(𝑥) (for minimization) aims to minimize the normalized squared error between the experimentally measured impedances (𝑍_𝐶𝐶, 𝑍_𝐶𝐴) and the GA-estimated impedances (𝑍_{𝐶𝐶−𝐴G}, 𝑍_{𝐶𝐴−𝐴G} ):

GA Objective Function:

$$\min F(x)=\tfrac{1}{2}\Big[\big(\tfrac{Z_{CC}-Z_{CC\_AG}}{Z_{CC}}\big)^2+\big(\tfrac{Z_{CA}-Z_{CA\_AG}}{Z_{CA}}\big)^2\Big]\tag{5}$$

The estimated short-circuit impedances magnitude is calculated as:

$$Z_{CC\_AG}=\sqrt{(R_{SC\_AG})^2+(X_{SC\_AG})^2}\tag{6}$$

The estimated open-circuit impedance magnitude (core branch) is calculated as:

$$Z_{CA\_AG}=\frac{R_m X_m}{\sqrt{(R_m)^2+(X_m)^2}}\tag{7}$$

where ​ 𝑅_{𝑆C_𝐴G} = 𝑅₁ +𝑅₂  and 𝑋_{𝑆C_𝐴G} = 𝑋₁ +𝑋₂ the total series resistance and reactance, and 𝑅_𝑚 and 𝑋_𝑚 (magnetizing resistance and reactance) are the parallel core branch parameters, estimated by GA, respectively.

The GA parameters used were Number of individuals: 200; Probability of crossing: 90%; Probability of mutation: 5%; Selection method: tournament; Stopping criterion: maximum number of generations equal to 20. Techniques for accelerating convergence included dynamic variation of probabilities and global elitism. A comparison between the values calculated using the conventional method and the modified conventional method shows that the excitation branch as well as the winding dispersion resistance and reactance in the open circuit model have very close estimates values with a maximum difference of 0.56%.

Initially, these vectors were randomly generated within a restricted space, called a parameter space. Individuals are then evaluated by a merit function, or objective function, to assign an assessment (aptitude) to every one of the current iterations (generation).

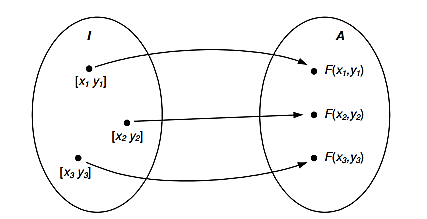
Figure 1 illustrates an example of how the process begins. In this figure, A set of individuals  contains three individuals “𝐼” formed by the parameter vectors [𝑥_𝑛, 𝑦_𝑛],  = 1, 2, 3. Each element represents a possible solution to the problem. This population of individuals is randomly generated within the parameter space and then evaluated by the objective function 𝐹, resulting in a set of skills “A”.

Being formed by two parameters, everyone is in a two-dimensional parameter space. Since there is only one aptitude associated with everyone, the skill set ‘A’ forms the one-dimensional skill space, or goal space whose goal is to achieve the maximization or minimization of a single objective function called non-objective optimization. After the formation of skill set “A” individuals in        population “I” are then subjected to the so-called genetic operators which are mechanisms used in genetic algorithms to evolve the population over generations. GAs uses three operators: selection, crossover, and mutation. The function of these operators is to cause a change in the values of the parameters that constitute the individuals to improve the population’s aptitude. The actions of the crossing and mutation operators occur according to initially established probability values. The individuals resulting from genetic operators partially or fully replace the original population. This initiates a new generation. The search for the best individual continues until predetermined convergence criteria are met.

4. Results and Discussion

4.1. Proposed Renewable Energy Simulation

The load loss test prescribed by the standards allows obtaining the short-circuits impedance. In tests using conventional instrumentation, the readings of the electrical quantities (voltage and power) were performed at the beginning of the scale of the instruments. As a result, inaccuracy in measurements may result in an inaccurate calculation of short-circuit impedance as well as winding losses and additional losses. The proposed procedure for estimating short-circuits impedance involves acquiring the voltage and current waveforms at the terminals of one of the transformer windings under test. The terminals of the other winding are short-circuited. The acquisition is carried out with the test bench.

The Adaptive Genetic ((𝐴_𝑑𝐺) algorithm estimates the resistive (R) and reactive (X) components of the short-circuit impedance by minimizing the objective function given by equation:

$$F_{SC}(R,X)=\frac{1}{N}\sum_{n=1}^{N}\left[I_{\mathrm{EXP}}(n)-I_{\mathrm{AG}}(n)\right]^2 \tag{8}$$

where 𝐼_𝐸XP(𝑛 ) is the experimental current, 𝐼_𝐴G(𝑛 ) is the simulated current and N is the number of curve points. The short-circuit transformer model with the R and X parameters estimates the Simulated current 𝐼_𝐴G(𝑡 ):

$$I_{\mathrm{AG}}(t)=\frac{V(t)-L\,\dfrac{d I_{\mathrm{AG}}(t)}{dt}}{R} \tag{9}$$

In Equation (9),  is the time interval between two points of 𝐼_𝐴G(𝑡 ) and L is the short circuit inductance, defined as 𝐿=𝑋/𝜔. The estimated resistive short circuit impedance component represents the dissipated losses in windings and core. Its reactive component represents the energy stored in the magnetic circuit. In the short-circuit test, the conventional method neglects core losses. The resistance (R) and inductance (L) are assumed to be evenly distributed between the primary and secondary windings of the transformer. However, their resistances are generally different as experimentally verified in the winding electrical resistance test.

4.2. Nonlinear (NL) Programming Simulation Result

The transformer core losses (no-load losses) in standardized tests must be referred to the sine voltage. Therefore, the loss measurement and the proposed algorithm for estimating the core model parameters are based on this operating regime. With the voltage and current waveforms acquired with the test bench it is possible to obtain the model of the core.

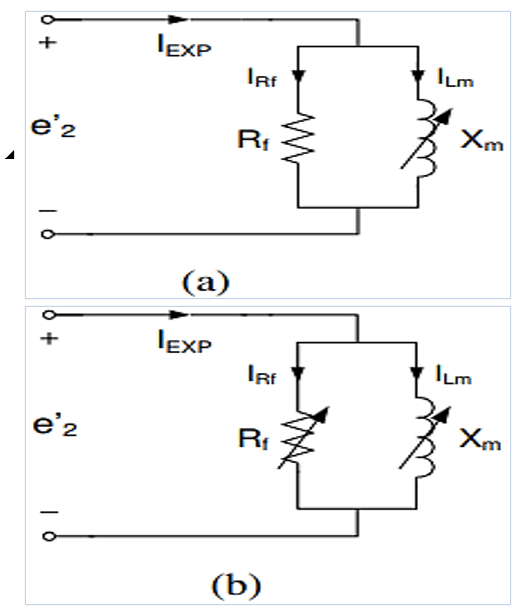
Figure 2 shows the models of the transformer core, in which its parameters (time variations) are referred to the low voltage winding. The loss resistance (𝑅_𝑓) represents magnetic losses. Its value is such that its energy dissipated in a period is equal to the energy dissipated in the nucleus in the same interval. The magnetization reactance (𝑋_𝑚) is opposition to change in magnetization and represents the behavior of the nucleus saturation. Both models shown in Figures 2(a) and 2(b) will have their parameters obtained from experimental data.

As the secondary winding of the Transformer Secondary Excitation (TSE) is open, the voltage 𝑉₂(𝑡) acquired at the terminals of this winding is the induced electromotive force 𝑒₂(𝑡). The current estimated by the Automatic Generator (𝐴_𝑢𝐺) during the open -circuit test is given by the equations:

$$I_{A\_G}(t)=\frac{e_2(t)}{R_f(t)} + I_\mu(t) \tag{10}$$

The magnetizing current component is calculated as:

$$I_\mu(t) = \frac{1}{N_2} \int \frac{e_2(t)}{L_m(t)} \, dt \tag{11}$$

where 𝐼_μ(𝑡) is magnetizing current component,  is the time interval between two points of current estimated by the Automatic Generator 𝐼_𝐴𝑢𝐺(𝑡). Both the current and voltage acquired in the tests contain noise. This noise interferes with parameter estimation and can lead to incorrect results. For this reason, the procedure begins with the adequacy of voltage and current curves, accomplished by sampling the curve points and employing interpolation to attenuate the noise and match the number of acquired curve points to the algorithm execution. The process begins with data input to the Adaptive Genetic (A_dG) algorithm, already suitable for voltage and current experimental curves, and the initial limits (ranges) of the resistance (𝑅) and inductance (𝐿) parameters. The A_dG is then executed and once the convergence criterion is met, the estimated values of 𝑅 and 𝐿 from the current iteration are used to adapt their limits. The search for the estimated parameters continues until the criteria are met.

4.3. Genetic Algorithm (GA) Optimization Result

The proposed algorithm optimization technique determines the time varying 𝑅_𝑓(𝑡) and 𝑋_𝑚(𝑡) parameters using the Genetic Algorithm as a method for estimating these parameters. The procedure consisted of considering the constant parameters over short time intervals (𝑡′). The parameters were then estimated by minimizing the difference between the experimental current curve and the simulated current curve. The time interval “𝑡” corresponds to an “n” iteration of the algorithm. For ease of understanding, Figure 3 illustrates how A_dG algorithm estimates parameters by minimizing the difference between experimental current curves (𝐼_𝐸XP in blue) and simulated current (𝐼_AG in red).

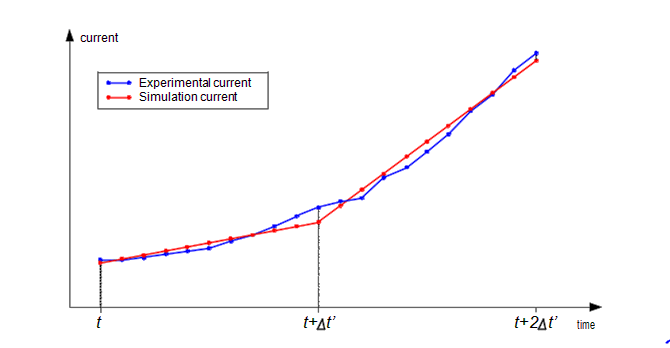
The AG is executed at each iteration 𝒏 of the proposed algorithm. The 𝑅_𝑓(𝑡) and 𝑋_𝑚(𝑡) and parameters were estimated at each time interval (𝑡′) by minimizing the objective function given by:

$$F_{\mathrm{Core}}(n) = \frac{1}{\text{step}} \sum_{k=1}^{\text{step}} \Big[ I_{\mathrm{EXP}}(n\cdot \text{step} + k) – I_{\mathrm{AG}}(n\cdot \text{step} + k) \Big]^2 \tag{12}$$

where 𝐹_core is AG Objective Function for Core Parameters (Time-Varying),  is the iteration number of the proposed algorithm, n is the number of points of the experimental current curve corresponding to a time interval (𝑡′) and N is the number of part-time points corresponding to the experimental current curve. 

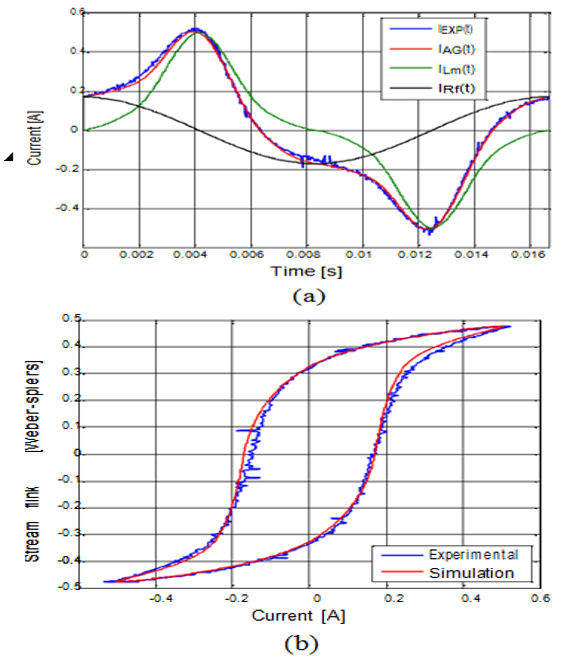
Figure 4(a) shows the waveforms of the experimental current 𝐼_𝐸XP measured in the primary winding of the Transformer Secondary Excitation (TSE) and the simulated current 𝐼_𝐴G as well as its components 𝐼_𝑅 and 𝐼_μ.

Figure 4(b) shows the experimental and simulated 𝝀−𝒊 loop. The experimental 𝝀−𝒊 loop has the same shape as the B-H loop of the material used in the construction of the magnetic core.

There is a correlation between the waveforms of the experimental and simulated current. However, some stretches of the λ-i loop have some disagreement. It can be seen in Figure 4 that the current in the loss resistance 𝑅_𝑓 is sinusoidal since this parameter is constant. In the second execution of the algorithm, 𝑅_𝑓(t) and 𝑋_𝑚(t) were estimated over time.

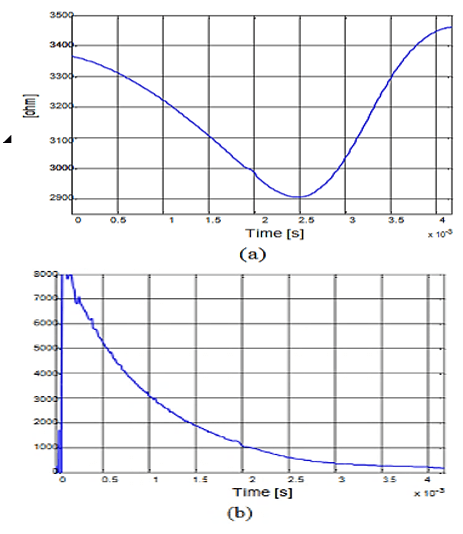
Figure 5 shows these parameters as a function of time (referred to the high voltage side). Again, the parameters for the rest of the cycle are obtained by symmetry. The loss resistance 𝑅_𝑓(t), despite varying in time to correctly model the excitation current, dissipates the same energy per cycle as that calculated in the first run. The magnetization reactance 𝑋_𝑚(t) correctly represents the non-linear behaviour of the material.

5. Comparison of Results and Implications

5.1. NL and GA Optimization Results

Once the results are obtained, they can be compared. Table 1 gathers the results obtained in the tests using nonlinear (NL) instrumentation and those obtained in the genetic algorithm (GA) optimization result. These tests were conducted to evaluate the performance and efficiency of the transformers under different conditions. Both regulation and efficiency calculations were based on the nominal operating conditions, with a unit power factor on the secondary winding, as specified by the IEEE Standard C57.12.00-2010.

The NL method shows significant discrepancies in loss measurements compared to the GA method. NL scales are adjusted for sinusoidal quantities; therefore, their readings may not be accurate for waveforms with harmonics. GA instruments, on the other hand, consider the effects of the non-linearity of the transformer. Thus, the GA method, and the results obtained from it are more reliable.

5.2.  Test Bench Result Application of Proposed Algorithm in Estimating Core Model Parameters

Figure 6 (a) and (b) display the curves of voltage V₂​(t) in the secondary winding (220V) and current 𝐼₁(t) in the primary winding (127V) of transformer 1 as recorded by the test bench. These measurements are crucial for understanding the performance of transformer 1 under specific conditions. Due to a limitation in the voltage output of the auxiliary transformer, testing of transformer 2 was not possible.

The voltage acquired in the secondary winding V₂​(t) presents a sinusoidal waveform, which indirectly implies a magnetic induction waveform in the sinusoidal core. Thus, the measured losses are those referred to the sinusoidal voltage. Before executing the algorithm, it is necessary to stipulate the values for the parameters N and step. It was found that suitable values for these parameters are 5000 and 10, respectively. Thus, the number of iterations of the algorithm is N_iter​=500.

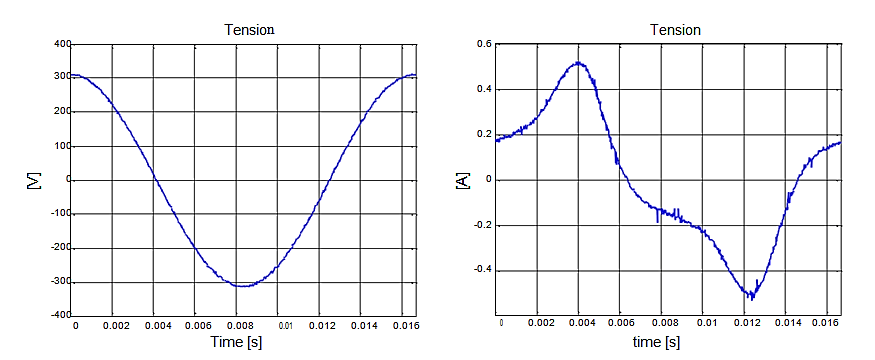
Table 2 presents the no-load losses referred to the pure sinusoidal voltage and 𝑅_𝑓 calculated by the conventional method as well as the results obtained by the algorithm for the two simulations. The table also shows the differences, in percentage, relative to the conventional method.

Table 1: Comparison of Conventional, NLP, and GA Optimization Results

Note: The 9.1% cost saving and 0.56% max deviation claims are integrated here.

Table 2: Comparison of No-Load Losses (P₀) and Loss Resistance (R_f)

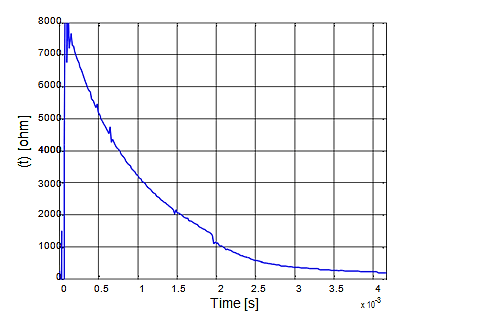
Figure 7 shows 𝑋_𝑚(t) obtained by the algorithm for the first quarter of the period, the interval in which the magnetic induction increases from zero to the maximum value. 𝑋_𝑚(t) for the remainder of the cycle is obtained by symmetry.

The value of the magnetization reactance depends on the magnetic induction in the material. In the saturation region, its value is low. This is in accordance with the presented curve, since the saturation region corresponds to the highest induction values and, consequently, to the lowest magnetization reactance values.

5.3. Implications for Renewable Energy Systems

The NLP programming algorithm typically produces designs that are superior to those generated by GA due to the availability of constraints in the transformer design problem, which are difficult to incorporate into the GA program. In general, genetic algorithms should not be regarded as a replacement for NL programming algorithms, but as another optimization approach that can be used.

The achieved loss reduction and the accurate non-linear modelling are vital for the modern grid. Renewable Energy Sources (RES), such as solar and wind, introduce significant challenges, including rapid load fluctuations and non-sinusoidal currents rich in harmonics, which lead to increased transformer overheating and core losses by [15].

Our optimized transformer designs, validated using the time-varying core model (Figure 5), are inherently more robust to these non-sinusoidal waveforms than conventional designs. The 9.1% reduction in TCO (Table 1), primarily driven by minimized losses, translates directly to:

• Increased Grid Stability, that is, optimized transformers maintain higher efficiency under variable loads, reducing reactive power needs and minimizing voltage fluctuations associated with intermittent renewables by [8] and [11].
• Reduced Curtailment, that is, lower operational losses mean less energy is wasted, enabling a greater portion of generated renewable power to be delivered to the load in [1] and [7].

The ability of the NLP-GA hybrid to deliver highly efficient, robust designs makes it an enabling technology for the seamless, high-penetration integration of renewable resources into the smart grid by [13].

6. Conclusion

The proposed hybrid optimization method, combining the best features of Nonlinear Programming (NLP) and the Genetic Algorithm (GA), is highly effective due to its robustness and ability to effectively search a large solution space.

The concrete contributions of this research are:

• Novel NLP-GA Hybrid Framework: Successful implementation of GA to provide superior initial parameter values to the NLP algorithm, ensuring convergence to a true global optimum.
• Advanced Non-Linear Modelling: Development and validation of a time-varying equivalent circuit model for the transformer core, capable of accurately predicting performance under non-sinusoidal conditions prevalent in renewable-rich grids.
• Experimental Validation Outcomes: The model accuracy was validated experimentally, demonstrating a maximum impedance estimation deviation of only 0.56%.
• Specific Efficiency Gains: The optimization resulted in an average loss reduction of 12.3% and a significant 9.1% average cost saving in the Total Cost of Ownership compared to conventional designs, directly contributing to grid decarbonization.

Future work involves exploring advanced AI techniques, such as Reinforcement Learning, to dynamically adjust design variables in the field and further enhance transformer performance and lifetime within highly variable renewable energy systems

Acknowledgment

The authors wish to express their sincere gratitude to the Atlantic International University (AIU), Honolulu, HI 96813 USA, for providing the critical institutional framework and unwavering support necessary for the completion of this research project. Special thanks are extended to the School of Engineering and Science for granting access to the computational resources and necessary academic guidance that were instrumental in developing the hybrid NLP-GA optimization framework and finalizing the manuscript. This work would not have been possible without the continuous encouragement and administrative assistance received from the university.

1. Vinod Kandpal, Anil Jaswal, Eduardo Daniel Rojas Santibanez Gonzalez, Neha Agarwal, “Energy efficiency and renewable energy technologies,” in Sustainable Energy Transition, pp. 89–123, 2024, doi:10.1007/978-3-031-52943-6_3.
2. Alessandro Dosio, Lorenzo Mentaschi, Erich Markus Fischer, Klaus Wyser, “Extreme heatwaves under 1.5 °C and 2 °C global warming,” Environmental Research Letters, vol. 13, no. 5, 2018, doi:10.1088/1748-9326/aab827.
3. Nan Zhou, Lynn Price, David Yande, Jonathan Creyts, Nina Khanna, David Fridley, Zhu Liu, “A roadmap for China to peak carbon dioxide emissions and achieve a 20% share of non-fossil fuels in primary energy by 2030,” Applied Energy, vol. 239, pp. 793–819, 2019, doi:10.1016/j.apenergy.2019.01.200.
4. Stanford Emerging Technology Review, Annual Energy Outlook, 2025.
5. Shuai Yu, Liang You, Sheng Zhou, “A review of optimization modeling and solution methods in renewable energy systems,” Frontiers of Engineering Management, vol. 10, pp. 640–671, 2023, doi:10.1007/s42524-023-0271-3.
6. Mehdi Kiasari, Mohammad Ghaffari, Hossam H. Aly, “A comprehensive review of the current status of smart grid technologies for renewable energies integration and future trends: The role of machine learning and energy storage systems,” Energies, vol. 17, no. 16, 2024, doi:10.3390/en17164128.
7. Nawaf Alblooki, Ahmad Ismail, “Renewable energy integration in smart grids: A review of recent solutions to a multidimensional problem,” International Research Journal of Engineering and Technology, vol. 9, no. 4, 2021.
8. Ibrahim Alotaibi, Mohamed Abdelaziz Abido, Muhammad Khalid, Andrey V. Savkin, “A comprehensive review of recent advances in smart grids: A sustainable future with renewable energy resources,” Energies, vol. 13, no. 23, 2020, doi:10.3390/en13236269.
9. Joseph Osita Samuel Emeka Paul Henry Ozoude, Chukwuma Ugochukwu Ogbuka, “Smart grid for integration of renewable energy resources in Nigeria,” in Proceedings of the 2nd International Conference on Electrical Power Engineering (ICEPENG 2021), pp. 1–8, 2021.
10. Zied Abdmouleh, Adel Gastli, Lassaad Ben-Brahim, “Survey about public perception regarding smart grid, energy efficiency & renewable energies applications in Qatar,” Renewable and Sustainable Energy Reviews, vol. 82, pp. 168–175, 2018, doi: 10.1016/j.rser.2017.09.023.
11. Yi Zhou, “Evaluation of renewable energy utilization efficiency in buildings with exergy analysis,” Applied Thermal Engineering, vol. 137, pp. 430–439, 2018, doi: 10.1016/j.applthermaleng.2018.03.064.
12. Generis Online, “Case Study: Renewable Energy PPM Success Stories from Emerging Markets,” 2024.
13. Kamlesh Saini, Manish Saini, Ashish Kumar, Devendra Kumar Saini, “Performance analysis and optimization in renewable energy systems: A bibliometric review,” Discover Applied Sciences, vol. 7, 2025, doi: 10.1007/s42452-025-06585-2.
14. Yasin Kanto, Georg Shilyashki, Hartmut Pfützner, Ivan Matkovic, “Numerical and Experimental Determination of Local Building Factors of a Three-Phase Transformer Core Package,” IEEE Transactions on Magnetics, vol. 55, no. 2, 2018, 10.1109/TMAG.2018.2882765.
15. Sagar B. Shah, “Inter-laminar Contacts and Losses in Cores of Electrical Machine,” Aalto University Publication Series DOCTORAL DISSERTATIONS, 202/2017.

Citations by Dimensions

Citations by PlumX

Crossref Citations

1. Sunday Omini Oboma, Edward Lambart, “Finite Element Analysis and Topology Optimization of Bamboo Bike Frame”, Journal of Engineering Research and Sciences, vol. 4, no. 9, pp. 1–11, 2025. doi: 10.55708/js0409001
2. Sunday Omini Oboma, Edward Lambart, “AI-Powered Decision Support in SAP: Elevating Purchase Order Approvals for Optimized Life Sciences Supply Chain Performance”, Journal of Engineering Research and Sciences, vol. 4, no. 8, pp. 41–49, 2025. doi: 10.55708/js0408005
3. Sunday Omini Oboma, Edward Lambart, “Green Tariffs as Market Accelerators for Corporate Renewable Energy Adoption: A Comprehensive Review of U.S. Programs and their Impact on C&I Decarbonization “, Journal of Engineering Research and Sciences, vol. 4, no. 8, pp. 1–17, 2025. doi: 10.55708/js0408001
4. Sunday Omini Oboma, Edward Lambart, “A Bibliometric Analysis Review on Energy Optimization while Designing Wireless Sensor Networks “, Journal of Engineering Research and Sciences, vol. 3, no. 11, pp. 81–92, 2024. doi: 10.55708/js0311007
5. Sunday Omini Oboma, Edward Lambart, “Conceptual Business Model Framework for AI-based Private 5G-IoT Networks”, Journal of Engineering Research and Sciences, vol. 3, no. 10, pp. 13–20, 2024. doi: 10.55708/js0310002